Özel Tanımlı Fonksiyonlar Konu Anlatımı Video

LYS Sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan ve matematik 2 diye tabir edilen alanda yer alan matematik Özel Tanımlı Fonksiyonlar online ders anlatımı yapan gözde hocaların Özel Tanımlı Fonksiyonlar konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Özel Tanımlı Fonksiyonlar video konu anlatımlarını listeledik, Değerli okuyucumuz LYS için olan ve mat 2 konuları arasında yer alan online matematik Özel Tanımlı Fonksiyonlar konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Özel Tanımlı Fonksiyonlar konusu ile ilgili yazılı anlatım ve genel Özel Tanımlı Fonksiyonlar formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.) Özel Tanımlı Fonksiyonlar Konu Anlatımı Videolar

Matematik Özel Tanımlı Fonksiyonlar Konu Anlatımı Yazılı

Bu ders notumuzda bir çok sınavda karşımıza çıkan Matematik Özel Tanımlı Fonksiyonlar konusunun geniş konu anlatımını, konun önemli yerlerini bulabilirsiniz.

A. BİR FONKSİYONUN TANIM KÜMESİ

Kuralı verilmiş bir fonksiyonun tanımlı olduğu en geniş reel sayı kümesine o fonksiyonun tanım kümesi (tanım aralığı) denir.

1. Polinom Fonksiyonun Tanım Kümesi

f(x) = a_n xⁿ + a_{n – 1} x^{n – 1} + …+ a₁x + a₀

şeklindeki reel katsayılı polinom fonksiyonları bütün reel sayılar için tanımlıdır.

Tanım kümesi A ile gösterilirse, polinom fonksiyonlarının tanım kümesi 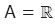olur.

2. Rasyonel Fonksiyonların Tanım Kümesi

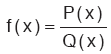şeklindeki rasyonel fonksiyonlar

Q(x) = 0 için tanımsızdır.

Q(x) = 0 denkleminin çözüm kümesi Ç = B ise f(x) fonksiyonunun en geniş tanım kümesi (tanım aralığı) 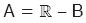olur.

ÖRNEK 1:

f(x)=√x²+3x+4a+1 fonksiyonu tüm reel sayılar için tanımlı ise a nedir ?

ÇÖZÜM 1:

x²+3x+4a+1≥0 olmalı burada ifadenin tüm reel sayılar için tanımlı olması için,

D≤0 olmalıdır. Çünkü D<0 ve eşitlik durumunda tabloda işaret değişmez. Tüm reel sayılarda tanımlı olur.

9-4.(4a+1)≤0 ise

a≥5/16 ise a nın değer aralığı [5/16,&) bulunur.

—————————————————————————-

ÖRNEK 2:

f(x)=√log₂(x-4)-5

fonksiyonun en geniş tanım aralığı nedir ?

ÇÖZÜM 2:

log₂(x-4)-5≥0 aynı zamanda x-4>0 , x>4 olmalı.

(x-4)≥32

x≥36 olur o halde tanım aralığı [36,&) olur.

3. Çift Dereceden Köklü Fonksiyonların Tanım Kümesi

n bir pozitif tam sayı olmak üzere, 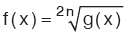şeklindeki fonksiyonlar g(x) ³ 0 için tanımlıdır.

g(x) ³ 0 eşitsizliğinin çözüm kümesi Ç = B ise f(x) fonksiyonunun en geniş tanım kümesi A = B dir.

4. Tek Dereceden Köklü Fonksiyonların Tanım Kümesi

n bir pozitif tam sayı olmak üzere,

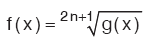
fonksiyonu, g(x) in tanımlı olduğu escort bakırköy her yerde tanımlıdır. g(x) in tanım kümesi B ise f(x) in tanım kümesi (aralığı) A = B dir.

Örnekler:

Aşağıdakilerin tek ve çift fonksiyon olma durumlarını inceleyelim.

f(x)=x⁴+5x²-7 fonksiyonunda çift kuvvetli bilinmeyenler olduğundan çift fonksiyondur.

f(x)=x⁵+x³ fonksiyonu tek kuvvetli bilinmeyenlerden oluştuğu için tek fonksiyondur

f(x)=x²-x fonksiyon ne tektir ne de çifttir.

f(x)=x.|x| fonksiyonunun tek mi çift mi olduğunu anlamak için f(-x) durumunu inceleyelim. f(-x)=-x.|-x|=-f(x) olduğundan tek fonksiyondur.

—————————————————————————————————————

SORU 1:

f(x) fonksiyonun grafiği orjine göre simetriktir.

f(x)+3f(-x)=x³+x

ise f(2)=?

ÇÖZÜM 1:

Grafiğin orjine escort bayan bakırköy göre simetrik olmasından fonksiyonun tek fonksiyon olduğunu anlarız.

f(-x)=-f(x) yazabliriz.

f(x)-3f(x)=x³+x

-2f(x)=x³+x

x=2 için f(2) fonksiyonunu bulalım.

-2f(2)=10 ise f(2)=-5 bulunur.

—————————————————————————–

SORU 2:

f(x) fonksiyonun grafiği y eksenine göre simetriktir.

f(x)-x².f(-x)=5x

ise f(4)=?

ÇÖZÜM 2:

Fonksiyonun grafiği y eksenine göre simetrik ise fonksiyon çift fonksiyondur.

f(-x)=f(x) yazalım.

f(x)-x².f(x)=5x ise f(x)[1-x²]=5x olduğuna göre x=4 yazarsak,

f(4)=20/-15=-4/3 bulunur.

——————————————————————————-

SORU 3:

f(x)=(a-2)x³+x²+(4-b)x+3 fonksiyonu çift fonksiyon ise a.b=?

ÇÖZÜM 3:

Fonksiyon çift fonksiyon olduğuna göre, derecesi tek olan ifadelerin katsayılarını 0 yapmalıyız.

O halde a=2 ve b=4 olur. a.b=8 bulunur.

————————————————————————–

SORU 4:

f(x) tek fonksiyon g(x) çift fonksiyon olmak üzere,

f(-5)=3, g(3)=7 ise g(f(5))+g(-3) ifadesinin eşiti nedir ?

ÇÖZÜM 4:

f(-x)=-f(x)
g(-x)=g(x) şeklindedir.

f(-5)=-f(5) =>f(5)=-3 olur.

g(-3)+g(-3)=2g(-3)=2.7=14 bulunur.

B. PARÇALI FONKSİYONLAR

Tanım kümesinin alt aralıklarında farklı birer kuralla tanımlanan fonksiyonlara parçalı fonksiyonlar adı verilir.

C. MUTLAK DEĞER FONKSİYONU

f : A ® B fonksiyonu reel değerli bir fonksiyon olsun.

şeklinde tanımlanan |f| fonksiyonuna f fonksiyonunun mutlak değer fonksiyonu denir.

Kural

D. İŞARET FONKSİYONU

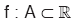den 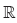ye bir fonksiyon olmak üzere,

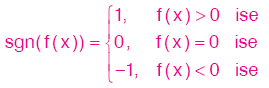
şeklinde tanımlanan fonksiyona f nin işaret fonksiyonu denir.

E. TAM DEĞER FONKSİYONU

1. Tam Değer Kavramı

x bir reel sayı olmak üzere, x ten büyük olmayan en büyük tam sayıya x in tam değeri denir ve 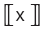ile gösterilir. x bir reel sayı olmak üzere, x ten büyük olmayan en büyük tam sayı t ise,

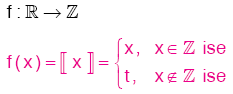
olur.

2. Tam Değer Fonksiyonu

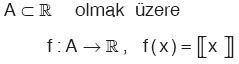
şeklinde tanımlanan fonksiyona tam değer fonksiyonu denir.

Kural

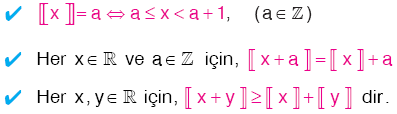SORU 1:

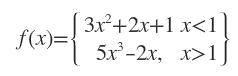
olduğuna göre f(2)+f(-1) kaçtır ?

ÇÖZÜM 1:

x=2 olması 2. ifadede 2 değerini yazacağımızı gösterir. f(2)=5.2³-4=40
x=-1 olması 1. ifadede -1 değerini yazacağımızı gösterir. f(-1)=3.(-1)³+2.(-1)+1=-4
40-4=36 bulunur.

—————————————————————————

SORU 2:

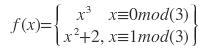
olduğuna göre f(3).f(4)-f(3) ifadesinin sonucu kaçtır ?

ÇÖZÜM 2:

f(3) ifadesinde x=3 değeri 1. ifadede 3 yazmamızı gerektirir, çünkü 3 mod3 de 0 kalanını verir. x yerine 3 yazarsak ifade 9 olur.
f(4) ifadesi için x=4 yazdığımızda mod 3 de 1 kalanını verir o halde 4²+1=17 olur.

9.17-9=144 bulunur.

——————————————————————————

SORU 3:

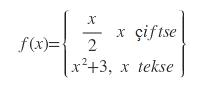
olduğuna göre fofof(1) kaçtır ?

ÇÖZÜM 3:

f(f(f(1))) ifadesi soruluyor.

f(1) için 1 tek olduğundan 2. de yerine yazarız. 1+3=4 olur.

f(4) için 4 çift olduğundan 1. de yerine yazarız 4/2=2 olur.

f(2) için 2 çift olduğundan 1. de yerine yazarız 2/2=1 olur.

f(2) son elde edeceğimiz sonuç olduğundan cevap 1 dir.

————————————————————————-

SORU 4:

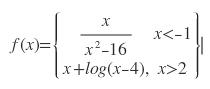
fonksiyonu hangi değerler için tanımsızdır ?

ÇÖZÜM 4:

x²-16=0 olursa 1. ifade için tanımsız yapan değeri buluruz
x=±4 için tanımsızdır ancak 1. ifade için aralık x<-1 olduğundan -4 değerini alırız.

x-4≤0 olursa 2. ifade için tanımsız yapan değerler bulunur.
burada x=3,4 değerleri için tanımsızdır.

fonksiyon -4,3,4 değerleri olmak üzere 3 değer için tanımsızdır.

SORU 5:

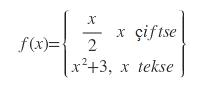
olduğuna göre fofof(1) kaçtır ?

ÇÖZÜM 5:

f(f(f(1))) ifadesi soruluyor.

f(1) için 1 tek olduğundan 2. de yerine yazarız. 1+3=4 olur.

f(4) için 4 çift olduğundan 1. de yerine yazarız 4/2=2 olur.

f(2) için 2 çift olduğundan 1. de yerine yazarız 2/2=1 olur.

f(2) son elde edeceğimiz sonuç olduğundan cevap 1 dir.

————————————————————————-

SORU 6:

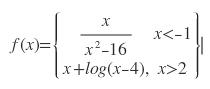
fonksiyonu hangi değerler için tanımsızdır ?

ÇÖZÜM 6:

x²-16=0 olursa 1. ifade için tanımsız yapan değeri buluruz
x=±4 için tanımsızdır ancak 1. ifade için aralık x<-1 olduğundan -4 değerini alırız.

x-4≤0 olursa 2. ifade için tanımsız yapan değerler bulunur.
burada x=3,4 değerleri için tanımsızdır.

fonksiyon -4,3,4 değerleri olmak üzere 3 değer için tanımsızdır.

Örnek:7

Örnek:

ÇÖZÜM 7:

Not:Parçalı fonksiyonlarda her fonksiyon tanımlandığı aralıkta çizilir.

    f(x)=-x  fonksiyonu x<2  aralığında tanımlandığından 2den büyük kısmını sileriz. f(x)=-10  fonksiyonu   2 ve 2 den büyük aralıkta tanımlandığın için bu aralıktaki kısmını alırız.

Burada bulunan Matematik Özel Tanımlı Fonksiyonlar Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]