Modüler Aritmetik Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Modüler Aritmetik online ders anlatımı yapan gözde hocaların Modüler Aritmetik konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Modüler Aritmetik video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Modüler Aritmetik konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Modüler Aritmetik konusu ile ilgili yazılı anlatım ve genel Modüler Aritmetik formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Modüler Aritmetik Konu Anlatımı Videolar
Matematik Modüler Aritmetik Konu Anlatımı 2 Ekol Hoca
Matematik Modüler Aritmetik Konu Anlatımı 2 TeknoFem
[t2]
Sitemizde Aşağıda yer alan Matematik Modüler Aritmetik Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Modüler Aritmetik canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.
Matematik Modüler Aritmetik Konu Anlatımı Yazılı
Tanım: a, b, m birer tam sayı ve m > 1 olmak üzere, tam sayılar kümesi üzerinde tanımlanan,
ß = {(a, b) : m, (a – b) yi tam böler}
bir denkliktir. ß denklik bağıntısı olduğundan, her (a, b) € ß için,
a ≡ b (mod m) biçiminde yazılır ve ” m modülüne göre a sayısı b ‘ye denktir. ” denir.
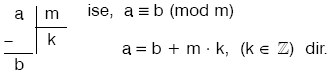
- Tam sayıların m sayma sayısı ile bölünmesiyle elde edilen kalanlar; 0, 1, 2, 3, 4, … , (m – 1) ‘dir.
Kritik Nokta: Her tam sayı m ile bölündüğünde hangi kalanı veriyorsa o kalana denktir. Bu kalanların her biri, belirlediği denklik sınıfının temsilci elemanı olarak alınırsa, denklik sınıfları;
![]()
olarak ifade edilebilir. Bu denklik sınıflarının kümesine m nin kalan sınıflarının kümesi denir ve biçiminde gösterilir. Buna göre;
![]()
Kritik Nokta:
n bir sayma sayısı ve k bir tam sayı ve
a ≡ b (mod m)
c ≡ d (mod m) olmak üzere,
- a + c ≡ b + d (mod m)
- a – c ≡ b – d (mod m)
- a × c ≡ b × d (mod m)
- an ≡ bn (mod m)
- a – b ≡ 0 (mod m)
- k × a ≡ k × b (mod m)
- n sayma sayısı; a, b, m sayılarının ortak böleni ise
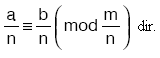
- a ile m ve b ile m aralarında asal olmak üzere,

Kritik Nokta: x, m nin tam katı olmayan pozitif bir tam sayı ve m bir asal sayı ise, xm–1 ≡ 1 (mod m)dir.
x in (m – 1) den daha küçük kuvvetinde de 1 bulunabilir. x ile m aralarında asal sayılar olmak üzere, m nin asal çarpanlarının kuvvetleri biçiminde yazılmış hali; m = ak . b r . c p olmak üzere

m asal sayı ise, (m – 1)! + 1 ≡ 0 (mod m) dir.
–27’nin 5 ile bölümünden kalan 2’dir. Bu ifade 27 ≡ 2 (mod 5) ile gösterilir.
–60’nın 10 ile bölümesinde kalan 0’dır. Bu ifade 60 ≡ 0 (mod 10) ile gösterilir.
–45’in 7 ile bölümünden elde edilen kalan 4’dür. Bu ifade -45 ≡ 4 (mod 7) ile gösterilir.
Özellikler :
1)
| x ≡ k (mod m) x-k ≡ 0 (mod m) |
} | 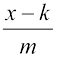 → Tam bölünür. → Tam bölünür. |
2) a,b,c,d ∈ Z ve m Z+-{1} olmak üzere
c ≡ d (mod m) ise
* a ± c ≡ b ± d (mod m)
* a.c ≡ b.d (mod m)
3) a ≡ b + k.m (mod m), k ∈ Z
4) k.a ≡ k.b (mod m),
5) an ≡ bn (mod m) n ∈ N
NOT : a ≡ b (mod m) iken, a ve m asal sayı ise
- Matematik Modüler Aritmetik Çözümlü soruları izlemek ve Modüler Aritmetik İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Modüler Aritmetik Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]
















