Matris Determinant Çözümlü Sorular ve Formüller

LYS sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Matris Determinant online soru çözümleri yapan gözde hocaların Matris Determinant çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik Matris Determinant cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda LYS matematik 2 konuları içinde yer alan online matematik Matris Determinant online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik Matris Determinant formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik Matris Determinant Çözümlü Sorular Videolar
Matematik Matris Determinant Çözümlü Sorular 2
Matematik Matris Determinant Çözümlü Sorular 3
Matematik Matris Determinant Çözümlü Sorular 2
Matematik Matris Determinant Formüller
MATRİSİN TANIMI
i, j, m, n sayma sayıları; i ≤ m, j ≤ n ve her i, j için aij reel sayılar olmak üzere,
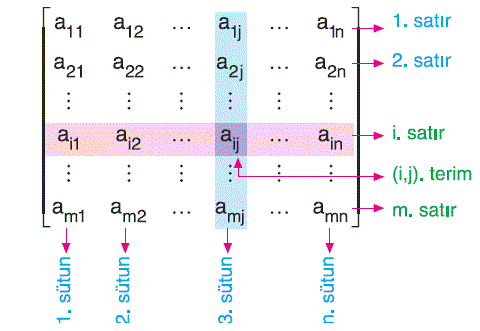
şeklinde, bir cismin elemanlarının sıralı bir tablosuna m ´ n türünde (m tane satır ve n tane sütun) bir matris denir.
Matrisler büyük harfle gösterilir. Tablodaki yatay sıralara satır, düşey sıralara sütun adı verilir.
Sıfır Matrisi
Bütün elemanları sıfır olan matrise sıfır matrisi denir.
Birim Matris
Kare matriste asal köşegen dışındaki bütün elemanları sıfır matrise birim matris denir. (Çarpma işlemine göre)

Bir Matrisin Devriği (Transpozesi)
Bir matrisin devriği (transpozu) satırların sütun, sütunların satır haline getirilmesiyle elde edilen matristir. Bir A matrisinin transpozu AT ya da Ad biçimlerinden biri ile gösterilebilir.
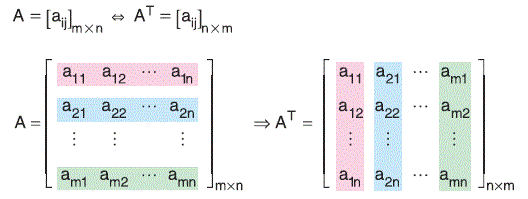
Kare Matrisin Çarpma İşlemine Göre Tersi
Aynı türden Ave B matrisleri ile 1 birim matrisi için:
AB = BA = 1 (birim matris) koşulunu sağlayan A ve B matrisleri varsa B matrisine, A matrisinin çarpma işlemine göre tersi denir. Bu durumda A’ da B’ nin tersidir. (B-1=A)
Kural
Bir A karesel matrisin tersini bulmak için A nın ek matrisi bulunur. Sonuç A nın determinantına bölünür.
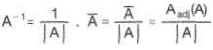
Bir matrisin tersinin olması için, matrisin karesel ve determinantının kesinlikle sıfırdan farklı olması gerekir.
Bir Matrisin Çarpma İşlemine Göre Tersi
A = [Aij]m×m biçimindeki kare matrislerin, çarpmaya göre tersini A–1 biçiminde gösteririz.
Determinantı sıfırdan farklı matrislerin tersi vardır.
|A| = (1/|A|).Ek(A) (|A| ≠ 0)
Kural
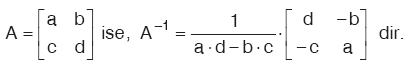 |
Özellik
|
İki Matrisin Toplamı
Satır ve sütün sayısı eşit iki matris toplanırken karşılıklı elemanlar toplanır.
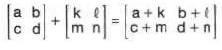
İki Matrisin Çarpımı
Ave B gibi iki matrisin çarpımlarının tanımlı olabilmesi için; A matrisinin sütun sayısının B matrisinin satır sayısına eşit olması gerekir.
[A]m.n ise [B]n.p olmalıdır. [A].[B] = [A.B]m.p dir.
Çarpım Yapılırken;
1. A’ nın 1. satırelemanları B’ nin 1. sütun elemanları ile çarpılıp toplanır. Bu AB çarpım matrisinin birinci elemanıdır. (a11)
2. A’ nın 1. satırelemanları B’ nin 2. sütun elemanları ile karşılıklı çarpılıp toplanarak çarpım matrisinden a12 elemanı elde edilir.
3. Bu çarpım A marisinin bütün satırları B matrisinin bütün sütunları ile çarpılıp mx; türündeki yeni matis elde edilinceye kadar devam eder.
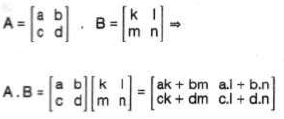
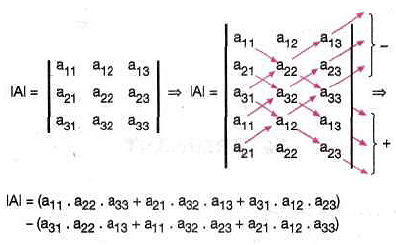
Sarrus Kuralı Yöntemi
3. mertebeden determinantın hesabı için geçerli bir kuraldır.
Determinant Nedir? Determinant Hesaplama
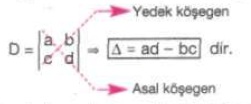
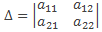 biçiminde verilen bir kalıba 2. mertebeden bir determinant denir.
biçiminde verilen bir kalıba 2. mertebeden bir determinant denir.Burada:
a11, a12 : Birinci satır
a21, a22 : İkinci satır
a11, a21 : Birinci sütun
a12, a22 : İkinci sütun
Determinant elemanlarını aij ile gösterisek,
i : Satır numarası,
j : Sütün numarasıdır.
Örneğin: a34 elemanı 3. satır, 4. sütün elemanı olur.Determinantın AçılımıBir determinant herhangi bir satıra (veya sütüna) göre açılımı, o satır elemanlarının kofaktörleri ile çarpımlarınn topamına eşittir. Buna determinantın değeri denir.
i = 1,2,3,…,m ve j = 1,2,3,…,n olmak koşulu ile aij gerçel sayılarının meydana detirdiği tabloya, m x n türünde matris denir.
Matisler [], (), || sembolleri arasına elemanların yazılmasıyla belirtilirler.
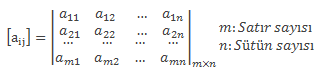
Minör
A bir kare matris, A matrisinin i’ninci satırının j’ninci sütunundaki eleman aij olsun. A matrisinin herhangi bir aij elemanının ait olduğu satır ve sütundaki elemanların silinmesi sonucu elde edilenmatrisin determinantına, aij elemanının minörü denir ve Mij ile gösterilir.
İşaretli Minör (Kofaktör)
Bir kare matriste aij elemanının minörü Mij olsun.
aij elemanının işaretli minörü (kofaktörü):Aij = (-1)i+j.Mij
Kural
| A=[aij]mxn matrisi verilsin. Bir matrisin determinantı, bu matrisin herhangi bir satır veya sütun elemanları ile bu elemanların işaretli minörlerinin çarpımlarının toplamına eşittir.i. satıra göre determinant:|A| = ai1.|A| = ai1.Ai1 + ai2.Ai2 + … + ain.Ain + ai2.Ai2 + … + ain.Ainj. sütuna göre determinant: |A| = a1j.A1j + a2j.A2j + … + anj.Anj |
- Matematik Matris Determinant Konu Anlatımlarını izlemek ve Matris Determinant İle İlgili Yazılı konu anlatımına Ulaşmak İçin Tıklayınız
- LYS Matematik konu Anlatımları ve Çözümlü Sorular (MAT 2) için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Matris Determinant Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















