Diziler Seriler Çözümlü Sorular ve Formüller

LYS sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Diziler Seriler online soru çözümleri yapan gözde hocaların Diziler Seriler çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik Diziler Seriler cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda LYS matematik 2 konuları içinde yer alan online matematik Diziler Seriler online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik Diziler Seriler formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik Diziler Seriler Çözümlü Sorular Videolar

Sitemizde yukarıda yer alan Matematik Diziler Seriler soru çözümleri gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Diziler Seriler canlı çözümlü örneklerin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.

Matematik Diziler Seriler Formüller

 DİZİLER

A boş olmayan bir küme olmak üzere, doğal sayıların bir alt kümesinden A’nın bir alt kümesine giden fonksiyonlara dizi denir. Eğer A, reel sayılar kümesi ise; bu diziye, reel sayılar dizisi denir.

Bir a dizisinin, n doğal sayısını götürdüğü değer, a_n ile ifade edilir ve bu dizi {a_n} şeklinde ifade edilir. Buradaki n sayısına dizinin indisi veya indeksi denir.

Bir dizinin, herhangi bir n doğal sayısı için değerine dizinin genel terimi adı verilir.

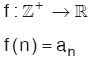fonksiyonununda,

olduğuna göre, biçiminde yazılabilir.

f fonksiyonu (dizisi) genel olarak,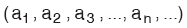biçiminde veya kısaca (a_n) biçiminde gösterilir.

a₁, dizinin 1. terimi (ilk terimi);

a₂, dizinin 2. terimi;

a₃, dizinin 3. terimi;

…

a_n, dizinin n. terimi (genel terimi) dir.

Uyarı

1. Genel terimi belirtilmeyen sayı grupları dizi meydana getirmezler.
2. Diziler değer kümesine göre adlandırılır.

Değer kümesi; reel sayılar kümesi olan dizi reel sayı dizisi, karmaşık sayılar olan dizi karmaşık sayı dizisi adını alır.

SONLU DİZİ

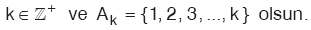 Tanım kümesi A_k olan dizilere sonlu dizi denir.

SABİT DİZİ

Bütün terimleri birbirine eşit olan diziye sabit dizi denir.

EŞİT DİZİ

Her n pozitif tam sayısı için, a_n = b_n ise, (a_n) ve (b_n) dizilerine eşit diziler denir.

SINIRLI DİZİLER

Bir {a_n} dizisinin tanım kümesindeki her n doğal sayısı için, t ≤ a_n olacak biçimde bir t değeri varsa; {a_n} dizisine alttan sınırlı dizi, t değerine ise {a_n} dizisi için bir alt sınır denir.

Bir {a_n} dizisinin tanım kümesindeki her n doğal sayısı için, a_n ≤ s olacak biçimde bir s değeri varsa; {a_n} dizisine üstten sınırlı dizi, s değerine ise {a_n} dizisi için bir üst sınır denir.

Alttan ve üstten sınırlı bir diziye sınırlı dizi denir. Alttan veya üstten sınırlı olmayan bir diziye ise sınırsız dizi denir.

Alttan sınırlı bir dizinin en büyük alt sınırına (EBAS), dizinin infimumu denir.

Üstten sınırlı bir dizinin en küçük üst sınırına (EKÜS), dizinin supremumu denir.

DİZİLERLE YAPILAN İŞLEMLER

(a_n) ve (b_n) birer dizi, c bir reel sayı olmak üzere,

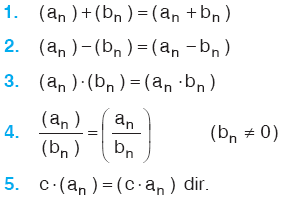
MONOTON DİZİLER

Genel terimi a_n olan bir dizide eğer her 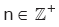için,

Uyarı

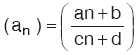dizisinin monotonluk durumuaşağıdaki şekilde incelenir:

1)Paydanın kökü (cn + d = 0 denkleminin kökü) 1 den küçük ise dizi monotondur.

Bu durumda,

a)ad – bc > 0 ise dizi monoton artandır.

b)ad – bc < 0 ise dizi monoton azalandır.

c)ad – bc = 0 ise dizi sabit

2)Paydanın kökü (cn + d = 0 denkleminin kökü) 1 den büyük ise dizimonoton değildir.

ALT DİZİ

Bir (a_n) dizisi verilmiş olsun. (k_n) artan bir pozitif tam sayı dizisi olmak üzere, 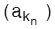dizisine (a_n) dizisinin alt dizisi denir ve 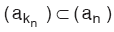biçiminde gösterilir. yani bir dizinin, elemanlarının sırasını bozmayacak biçimde bazı elemanlarını silerek ya da hiçbir elemanını silmeyerek elde edilen yeni diziye, o dizinin alt dizisi denir.

ARİTMETİK DİZİ

Ardışık terimleri arasındaki fark sabit olan dizilere aritmetik dizi denir. Yani; c sabit bir reel sayı olmak üzere, her n doğal sayısı için {a_n} dizisi, koşulunu sağlıyorsa {a_n} dizisi, bir aritmetik dizidir.

İlk terimi, ve ardışık terimleri arasındaki farkı bilinen bir aritmetik dizinin genel terimi, formülü ile bulunabilir.

GEOMETRİK DİZİ

Ardışık terimlerinin oranı sabit olan dizilere geometrik dizi denir. Yani; c sabit bir reel sayı olmak üzere, her n doğal sayısı için {a_n} dizisi, koşulunu sağlıyorsa {a_n} dizisi, bir geometrik dizidir.

İlk terimi, ve ardışık terimleri arasındaki oranı bilinen bir geometrik dizinin genel terimi, formülü ile bulunabilir.

DİZİLERİN YAKINSAKLIĞI VE IRAKSAKLIĞI

Komşuluk

a ve e birer reel sayı ve e >0 olmak üzere,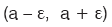 açık aralığına a nın e (epsilon) komşuluğu denir. Bu aralığı (kümeyi) T ile gösterirsek,

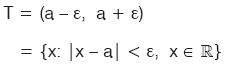olur.

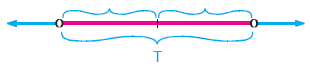
T kümesi sayı doğrusunda aşağıdaki gibi gösterilebilir.

Uyarı

1. (a_n) dizisinin, a nın e komşuluğundaki terimleri, 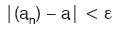eşitsizliğini sağlar.
2. (a_n) dizisinin, a nın e komşuluğu dışındaki terimleri, 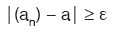eşitsizliğini sağlar.

YAKINSAK DİZİLER ve IRAKSAK DİZİLER

(a_n) bir reel sayı dizisi, a sabit bir reel sayı olsun.

Her e pozitif reel sayısı için, (a_n) dizisinin hemen hemen her terimi, a nın e komşuluğunda bulunuyorsa, (a_n) dizisi a ya yakınsıyor denir. (a_n) dizisi a sayısına yakınsıyorsa; (a_n) dizisine yakınsak dizi denir.

Yakınsak olmayan dizilere ıraksak diziler denir.

SERİLER

Herhangi bir (x_n) dizisinin sonlu tane elemanını değil de tüm elemanlarını “toplayalım”. x₁+ x₂ + … + x_n + … “toplamına” seri denir.

Bir (x_n) dizisi verilsin. Bu dizinin ilk n tane teriminin toplamı olan x₁+ x₂ + … + x_nifadesi sembolik olarak gibi yazılır. Buradaki Σ (sigma) harfi bu tür toplamları kısa olarak yazmak için kullanılır. k ya toplama indisi denir ve k indisi yerine başka indisin kullanılması sonucu etkilemez.
Şimdi (x_n) dizisinin sonlu tane elemanını değil de tüm elemanlarını “toplayalım”. x₁+ x₂ + … + x_n + … sonsuz “toplamına” seri denir.

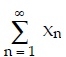
Sigma gösterimi yardımı ile bu seri gibi gösterilir. Şimdi sonsuz sayıda gerçel sayının toplamına anlam kazandırmak için

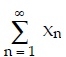
serisinden yeni (s_n) dizisini elde edelim:

s₁ = x₁ , s₂ = x₁+ x₂ , s₃ = x₁+ x₂ + x₃ , … , s_n = x₁+ x₂ + … + x_n , …

Eğer (s_n) dizisi yakınsak olup limiti a ise

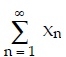
serisine yakınsak seri denir ve
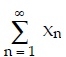=a

gibi yazılır. a sayısına serinin toplamı da denilir.
Eğer (s_n) dizisi ıraksak ise

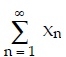
serisine ıraksak seri denir.

x₁ , x₂, … sayılarına serinin terimleri, x_n ye genel terimi, (s_n) dizisine serinin kısmi toplamlar dizisi denir.
Görüldüğü gibi sonsuz sayıda gerçel sayının “toplamı”, sonlu sayıdakilerin toplamlarının bir limiti olarak tanımlanmaktadır.

Burada bulunan Matematik Diziler Seriler Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.

[egit1]
[egit2]
[egit3]