Modüler Aritmetik Çözümlü Sorular ve Formüller

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Modüler Aritmetik online soru çözümleri yapan gözde hocaların Modüler Aritmetik çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik Modüler Aritmetik cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için istersenizde YGS LYS için olan online matematik Modüler Aritmetik online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik Modüler Aritmetik formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik Modüler Aritmetik Çözümlü Sorular Videolar
[t2]
Sitemizde Aşağıda yer alan Matematik Modüler Aritmetik soru çözümleri gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Modüler Aritmetik canlı çözümlü örneklerin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.
Matematik Modüler Aritmetik Formüller
MODÜLER ARİTMETİK
a, b sıfırdan farklı tamsayılar ve b>0 olmak üzere, a sayısını b ye bölmek demek, a = m.b+k, 0≤k
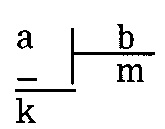
Bazı tam sayıların 3 ile bölme işlemini inceleyelim.
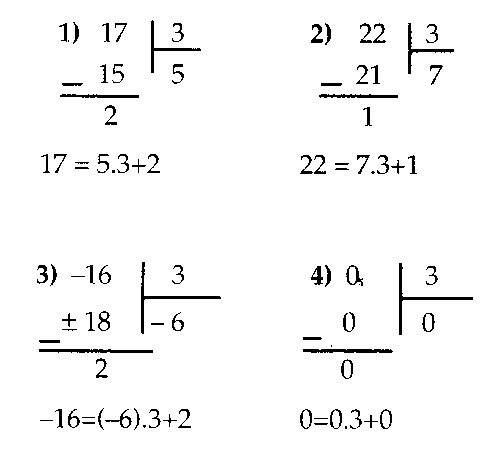
Sonuç: 3 ile bölümden kalanların 0,1,2 tamsayılardan biri olduğu görülüyor. Demek ki bir sayı 3 ile bölündüğünde 0,1,2 kalanlarını verir. Aşağıdaki kümeyi inceleyelim:

Burada; bir kümedeki her elemanın 3 ile bölümünden kalanın aynı olduğu, her kümedeki iki elemanın farkının 3 ile bölündüğünü ve bu kümelerin ayrık olup, birleşimlerinin de Zyi verdiğini görüyoruz.
Bu kümelerin z de
![]() bağıntısının denklik sınıfı oluşturduğunu biliyoruz.
bağıntısının denklik sınıfı oluşturduğunu biliyoruz.
![]() nin anlamı x-y = 3m (m∈Z) dir. Bu durum x = y (mod 3) yazılır ve “x’ denktir y modül 3″ diye okunur.
nin anlamı x-y = 3m (m∈Z) dir. Bu durum x = y (mod 3) yazılır ve “x’ denktir y modül 3″ diye okunur.
![]()
biçiminde yazılır. Bu ifade x ile k nın aynı denklik sınıfında olduğunu gösterir. Bu denklik sınıfı k ile gösterilir ve
![]() dir
dir
Tanım: a ve k tam sayıları ve m> o tamsayısı verilsin.
a-k farkı m ile tam bölünüyorsa, m modülüne göre a, k ya denktir denir ve a ≡ k (mod m) yazılır.
Yani, ![]()
Örnek: 3 Ι11-2 olduğundan
11 ≡ 2 (mod 3)
5 Ι12-(-3) olduğundan 12 ≡ -3 (mod 5)
5 Ι(-17)-(13) olduğundan
-17 ≡ 13 (mod 5)
3 modülüne göre kalan sınıfların kümesi Z/3,4 modülüne göre
Z/4, ……..m modülüne göre Z/m biçiminde gösterilir. bunlar,

Tanım:
Z/m kümesinin elemanlarına kalan sınıfları denir.
Uyarı: Z/m de toplama ve çarpma işlemlerinin değişme özeliği vardır.
Örnek: x ≡ 3 (mod5) ise x sayılarının kümesini bulunuz.
x ≡ 3 (mod5) <=> 5I x-3 => x -3 = 5k, k∈ Z => x = 3 +5k olur.
x∈ {…….-7, -2, 3, 8, 13……} bulunur.
Teorem:
a,b,c tam sayıları ve m pozitif bir tamsayı olsun.
1) a ≡ a (modm)
2) a ≡ b (modm) ise b ≡ a (modm)
3) a ≡ b (modm) ve b ≡ c (modm) ise a ≡ c (modm) dir.
Teorem:
a,b,c, de Z ve m ∈ Z+ için
1) a ≡ b (modm) ∧ c ≡ d (modm)
=> a±c =b±d (modm) dir.
2) a ≡ b (modm) ∧ c ≡ d (modm) => a.c ≡ b.d (modm) dir.
3) a ≡ b (modm) ise ak = bk(modm)
(k∈Z+)
4) pa ≡ pb (modm) p∈ Z
ÖRNEK:
****17 ≡ 2 (mod5) ve 28 ≡ 3(mod5) olduğundan
17+ 28 ≡ (2+3) (mod5) 45 ≡ 5 (mod5) 45 ≡ 0 (mod5)
O halde; mod(m) ye göre yazılmış iki denklik taraf tarafa toplanırsa, çıkarılırsa ya da çarpılırsa, yine bir denklik elde edilir.
****731993 sayısının birler basamağındaki rakamı bulunuz.
Çözüm: Bir sayının birler basamağındaki rakam, sayının 10 ile bölümünden kalandır.
731993 = x (modl0) dan x sayısını bulalım.
73 ≡ 3 (mod 10)
732 ≡ 9 (mod 10)
733 ≡ 7 (mod 10)
734 ≡ 1 (mod 10)
(734)498 ≡ (1)498 (mod 10)
731992 ≡ 1 (mod 10)
73 ≡ 3 (mod 10)
731993 ≡ 3 (mod 10)
Öyleyse sayının birler basamağındaki rakam 3 dür.
Uyarı:
a) Sayı, 1’e denk oluncaya kadar kuvvetleri alınır, 1’e denk olan kuvvete üs bölünür. Kalan üs olarak alınır.
b) m asal sayı ise 1 eksiği yani (m-1) inci kuvvetle mutlaka 1 bulunur ve tekrar başlar.
c) an = x (modm) de m ile a aralarında asal değilse 1 bulunmaz. Tekrar başlayıncaya kadar teker teker incelenir.
- Matematik Modüler Aritmetik Konu Anlatımlarını izlemek ve Modüler Aritmetik İle İlgili Yazılı konu anlatımına Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Modüler Aritmetik Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















