İşlem Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik İşlem online ders anlatımı yapan gözde hocaların İşlem konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik İşlem video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik İşlem konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik İşlem konusu ile ilgili yazılı anlatım ve genel İşlem formülleri de eklenmiştir.

Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen  yukarısında alt alta yer almaktadır.)İşlem Konu Anlatımı Videolar

Sitemizde Aşağıda yer alan Matematik İşlem Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik İşlem canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik İşlem Konu Anlatımı Yazılı

Fonksiyonların, A kümesindeki bir x elemanını verilen bir kurala göre B kümesindeki bir y elemanına eşlediğini öğrendik. İşlem de buna benzer olarak, fakat AxA dan aldığı elemanları verilen bir kurala göre B kümesindeki bir elemana eşlemektedir.Sonuç olarak işlem özel bir bağıntıdır. Verilen sıralı ikilileri tek bir elemana götürmektedir.
Tanım:
A ¹Æ ve AÌ Bolsun. AxA  nın boş kümeden farklı herhangi bir alt kümesinden     B ye tanımlanan her fonksiyona ikili işlem veya   işlem denir.

>İşlemler *,,D… gibi sembollerle gösterilir.

Not: AxA dan A ya tanımlanan fonksiyona A da işlem denir.

Örnek: Tam sayılar kümesi üzerinde tanımlanmış olan toplama, çıkarma, çarpma ve bölme işlemlerinin her biri bir işlemdir.

Örnek:
A ={1,2,3} o.ü. (x,y) ΠAxA  için x*y = x şeklinde tanımlanan * işleminin şemasını ve tablosunu çizelim.

AxA ={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)} o.ü.

1*1=1   2*1=2    3*1=3

1*2=1   2*2=2    3*2=3

1*3=1   2*3=2    3*3=3

Örnek: A ={0,1,2} ve  B ={-2,-1,0,1,2} o.ü.

kuralı ile verilen * işleminin tablosunu oluşturalım. inceleyelim.

0*0 = 0           1*0 = 1   2*0 = 2

0*1 = -1          1*1 = 0   2*1 = 1

0*2 = -2          1*2 = -1 2*2 = 0

Örnek: A ={-1,0,1} ve AxA nın bir alt kümesi

B={(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,0)} olmak üzere

*:B             A,         x*y = x+y işleminin şemasını ve tablosunu çiziniz.

Örnek: A ={0,2,4,6} kümesi üzerinde  x,y Î A için  x*y = 2x-y+1 biçiminde * işlemi tanımlanıyor. Buna göre aşağıdakileri bulunuz.

1. 0*2=?
2. 0*6=?
3. 4*0=?
4. 6*2=?
5. 6*4=?
6. 0*2 = 2.0-2+1 = -1
7. 0*6 = 2.0-6+1 = -5
8. 4*0 = 2.4-0+1 = 9
9. 6*4 = 2.6-4+1 = 9

Örnek: A ={-1,0,1,2,3} kümesi üzerinde tanımlanan * işleminin tablosu aşağıdaki gibidir. Buna  göre aşağıdaki istenen değerleri bulunuz.

-1*2 = ?

-1*-1 = ?

0*0 = ?

2*1 = ?

3*2 = ?

1*3 = ?

Çözüm

-1 * 2 = 0

-1 * -1 = -3

0 * 0 = 0

2 * 1 = 5

3 * 2 = 8

1 * 3 = 5

Örnek: Tam sayılar kümesi üzerinde tanımlanan

x*y = -x+2y ve xoy = x²+y   işlemleri için 1*(2o4) =? değerini bulunuz.

1 * (2o4) = 1 * ( 2²+4) = 1 * 8 = -1 +2.8 = -1 + 16 = 15  bulunur.

İŞLEMİN ÖZELİKLERİ

A. KAPALILIK ÖZELİĞİ

Tanım: *, A kümesinde tanımlı bir işlem olsun. “x,yÎ Aiçin x*y ÎA ise, A kümesi “*” işlemine göre kapalıdır denir.[“(x,y)Î Aiçin  x*y = z ÎA] olmalıdır.

Örnek: A ={0,1} kümesi üzerinde tanımlı x*y = x.y işleminin kapalı olup olmadığını inceleyiniz.

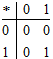
Küme sınırlı olduğu için  işlemin tablosunun çizelim.
Tablodan da görüldüğü gibi  “x,yÎ A için x * y Î Adır. Böylece A kümesi * işlemine göre kapalıdır.

Örnek: Ç ={0,2,4,6,….} kümesi üzerinde tanımlı x*y = x+y işleminin kapalı olup olmadığını inceleyiniz.

“x,yÎ Ç için x * y = x+y Î Ç oluyorsa  Ç kümesi * işlemine göre kapalıdır diyeceğiz. Ç den alacağımız elemanlar çift sayı olduğundan ve  iki çift  sayının toplamı daima çift sayı olduğundan * işlemine göre Ç kümesi kapalıdır.

B. DEĞİŞME ÖZELİĞİ

Tanım: *, boş olmayan A kümesi üzerinde tanımlı bir işlem olsun.
“x,yÎ A için    x*y = y*x oluyorsa * işleminin değişme özeliği vardır denir.

Örnek: Tam sayılar kümesi üzerinde tanımlı toplama işleminin değişme özeliği vardır fakat tam sayılar kümesi, üzerinde tanımlı çıkarma işleminin değişme özeliği yoktur.

Tam sayılar kümesi üzerindeki çıkarma işlemi

x * y = x – y dir. x * y = y  x olup olmadığına bakalım.

C. BİRLEŞME ÖZELİĞİ

Tanım: *,  boş olmayan A kümesi üzerinde tanımlı bir işlem olsun.
“x,y,zÎ A için   x*(y*z) = (x*y)*z oluyorsa * işleminin birleşme özeliği vardır denir.

Örnek: Tam sayılar kümesi üzerinde tanımlı toplama ve çarpma işlemlerinin birleşme özeliği vardır

Toplama işlemi            x * y = x + y

x * ( y * z ) = x * ( y +z ) = x + y + z = (x * y) +z = (x * y) * z

olduğundan toplama işleminin birleşme özeliği vardır.

Çarpma işlemi                          x * y = x.y

x * ( y * z ) = x *(y.z) = x.y.z = (x * y) .z = (x * y) * z

olduğundan çarpma işleminin birleşme özeliği vardır.

Örnek: Reel sayılar kümesi üzerinde tanımlı x*y = x+2y işleminin birleşme özeliği olup olmadığını inceleyiniz.

x * (y * z) = (x * y) * z

x *(y + 2z ) =(x + 2y ) *z

x + 2.(y + 2z) = x + 2y +2z

x + 2y + 4z = x + 2y +2z

eşitliği doğru olmadığından (çünkü sol tarafta 4z varken sağ tarafta 2z vardır) * işleminin birleşme özeliği  yoktur.

Örnek: Tam sayılar kümesi üzerinde tanımlı çıkarma ve bölme işlemlerinin birleşme özeliği olup olmadıklarını inceleyiniz.

Çıkarma işlemi            x * y = x – y

x * (y * z ) = (x * y) * z

x * (y – z ) = (x – y) * z

x – (y – z) = (x – y) – z

x – y + z = x – y – z

doğru bir eşitlik olmadığından  çıkarma işleminin birleşme özeliği yoktur. Benzer mantıkla bölme işleminin birleşme özeliği olmadığı da gösterilebilir.

Not: Bir işlemin birleşme özeliği varsa o işlem parantezlerden bağımsızdır. Yani bir * işleminin birleşme özeliği varsa

x * ( y * z ) = x * y * z yazılabilir.

D.DAĞILMA ÖZELİĞİ

Tanım: o ve *, boş olmayan A kümesi üzerinde tanımlı iki işlem olsunlar.
“x,y,zÎA için   x*(yoz) = (x*y)o(x*z)

oluyorsa * işleminin o işlemi üzerine soldan dağılma
“x,y,zÎA için(yoz)*x = (y*x)o(z*x)

oluyorsa * işleminin o işlemi üzerine sağdan dağılma özeliği vardır denir.

Örnek: Reel sayılar kümesi üzerinde tanımlı çarpma işleminin toplama ve çıkarma işlemleri üzerine dağılma özeliği vardır. (Hem sağdan hem de soldan)

E. ETKİSİZ (BİRİM) ELEMAN ÖZELİĞİ

Tanım: *, boş olmayan bir A kümesi üzerinde tanımlı bir işlem olsun.
“xÎ A için  x *e = e*x = x olacak biçimde bir   e  Î A varsa  e ye  “*” işleminin birim(etkisiz) elemanı denir.

Örnek: Tam sayılar kümesi üzerinde tanımlı x*y = x+y-3  işleminin birim elemanını bulunuz.

x * e = x   Þ  x + e + 3 = x   Þ   e + 3 = 0   Þ e = -3  bulunur.

Örnek: Tam sayılar kümesi üzerinde tanımlı x*y = x+2y-1 işleminin varsa birim elemanını bulunuz.

Teorem: *, A kümesi üzerinde bir işlem o.ü. * işleminin birim elemanı varsa en çok bir tanedir.

Örnek: A ={0,1,2} kümesi üzerinde tanımlı * işleminin tablosu alttaki gibidir.

Tabloya göre  *  işleminin birim elemanını bulunuz.

Bir işlemin tablosu verildiğinde, etkisiz elemanı bulurken, en soldaki sütunun aynısı ile en üstteki satırın aynısının kesiştiği yerdeki eleman etkisiz elemandır.

Yukarıdaki tabloya göre söz konusu satır ve sütunun  kesiştiği yerdeki eleman 2 olduğundan bu işlemin etkisiz elemanı e = 2 dir.

Not: Bir işlemin tablosu verildiğinde, baş satır ile baş sütunu veren satır ve sütunun kesiştiği eleman birim elemandır.

F. TERS ELEMAN

Tanım: A kümesi üzerinde tanımlı * işleminin birim elemanı e olsun.

Herhangi bir x Î A için   x*y = y*x = e  koşulunu sağlayan  bir  y ∈ A varsa, y elemanına * işlemine göre x in tersi denir. y = x^-1 ile gösterilir

Örnek:  Tam sayılar kümesinde tanımlanan toplama işlemine göre varsa (2) nin tersini bulunuz.

Toplama işleminin birim elemanı e = 0 olduğundan

2 * 2^-1 = 0  Þ  2 + 2^-1 = 0  Þ   2^-1 = -2  bulunur.

Örnek: Reel sayılar kümesi üzerinde tanımlı çarpma işlemine göre (4) ün tersini bulunuz.

Çarpma işleminin etkisiz elemanının e = 1 olduğunu biliyoruz. Böylece

Örnek: Reel sayılar kümesi üzerinde tanımlı   x o y = x+y+2xy  işlemine göre 3 ün tersini bulunuz.

Öncelikle bu işlemin birim elemanını bulmalıyız

x  * e = x  Þ x + e +2xe = x

e + 2xe = 0

e(1 + 2x) = 0

e = 0 bulunur.

e = 0 olduğuna göre  şimdi 3 elemanın tersini bulabiliriz.

3 * 3^-1 = 0   3 + 3^-1 + 2.3.3^-1 = 0

3 + 3^-1 + 6.3^-1 = 0

Teorem: *, A kümesi üzerinde tanımlı bir işlem olsun. * işlemine göre bir elemanın tersi varsa en çok bir tanedir.

Örnek: A ={1,2,3,4} kümesi üzerinde tanımlı * işleminin tablosu alttaki gibidir.

Buna göre 3^-1 ve 4^-1 bulunuz.

Tabloya göre * işleminin etkisiz elemanı e = 3 tür.

Bir işlemin tablosu verildiğinde bir elemanın tersini şöyle buluyoruz.

O elemanın en başta bulunduğu satırda birim elemana kadar ilerliyoruz ve birim elemana geldliğimiz sütunun en üstündeki eleman o elemanın tersidir.

Buna göre 3^-1 = 3 ve 4^-1= 2 dir.

Örnek: A ={a,b,c,d} kümesi üzerinde tanımlı  o işleminin tablosu altta verilmiştir.

1. e = ?
2. b.(a^-1)
3. d^-1
4. (b^-1o c)
5. (a o c)^-1
6. (c^-1)^-1

Çözüm

1. e = a
2. b. a^-1 = a
3. c. d^-1= b
4. (b^-1 o c) = (d o c) = b
5. e.(a o c)^-1 = c^-1 = c
6. f. (c^-1)^-1 = c^-1 = c  ( tersinin tersi kendisidir)

G.YUTAN ELEMAN

Tanım: *, boş olmayan A kümesi üzerinde bir işlem olsun.

∀x ∈ A için    x*y = y*x =y  olacak biçimde bir y∈ A varsa , y ye * işleminin yutan elemanı denir.

Örnek: Reel sayılar kümesi üzerinde tanımlı çarpma işleminin yutan elemanını bulunuz

x * y = y  Þ  x.y = y Þ y – xy = 0 Þ y(1 – x) = 0   Þ y = 0  bulunur.

Örnek: Reel sayılarda tanımlı  x*y = x + y –xy işlemine göre yutan elemanı bulunuz.

x * y = y   Þ  x + y –xy = y

x – xy = 0

x = xy

y = 1  olarak bulunur.

Not: Yutan elemanın tersi yoktur.

Burada bulunan Matematik İşlem Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]