Hız ve Hareket Problemleri Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Hız ve Hareket Problemleri online ders anlatımı yapan gözde hocaların Hareket Problemleri konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Hız ve Hareket Problemleri video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Hareket Problemleri konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Hareket Problemleri konusu ile ilgili yazılı anlatım ve genel Hareket Problemleri formülleri de eklenmiştir.

Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen  yukarısında alt alta yer almaktadır.)Hareket Problemleri Konu Anlatımı Videolar

Sitemizde Aşağıda yer alan Matematik Hareket Problemleri Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Hareket Problemleri canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik Hareket Problemleri Konu Anlatımı Yazılı

Birim zamanda gidilen yol, hız diye tanımlanmış.

yani;

1 saatte 60 kilometre gitmişsek hızımız 60 km/s olur.

1 dakikada 3 kilometre gitmişsek, hızımız 3 km/dk olur.

1 saniyede 2 metre gitmişsek hızımız 2 m/sn olur.

Hızı bulmak için ille de birim zamana göre aldığımız yolu hesaplamalıyız. Yani 3 saatte 90 kilometre gitmişsek, hızımız 90 km/s olmaz. Hız için 3 saatte değil, 1 saatte aldığımız yol önemlidir.

Zaten öyle olsaydı 90 kilometrelik yolu 3 saatte de alsak, 7 saatte de alsak hızımızın 90 km/s olması gerekirdi ki ne kadar saçma bir hareket olduğuna artık siz karar verin.

Süre arttıkça gidecek yol artacağından (mantığımız öyle söylüyor), süre ile yol doğru orantılıdır.

Bu sebeple, 3 saatte 90 kilometre giden biri, 1 saatte 30 kilometre gidebileceğinden hızı 30 km/s’tir.

Simdi bu işlemleri genelleyelim:

Bir hareketli x birimlik bir yolu, t birimlik bir sürede almış olsun Biz de bu hareketinin hızı olan V’yi bulmaya çalışalım. Bize t birim sürede aldığı yol değil, 1 birim sürede aldığı yol lazım.

O halde,

t birim sürede x birim yol gidiyorsa,

1 birim sürede V birim yol gider diye bir orantı kurarsak, ki bu doğru orantıdır, hareket linin hızının

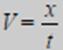olduğu çıkar.

İsteyen denklemi

veya

x = V.t gibi de ezberleyebilir ya da kullanabilir.

Ben olsam, x = V.t eşitliğini seçerdim, çünkü kesirli ifadeleri bilgisayarda yazması zor oluyor :))))

x = V.t esitliğini kocaman bir kağıda kocaman kocaman yazıp, odanızın duvarına asın!

Anneniz izin vermiyorsa da aklınızın bir kösesine yazın! Yani satırda değil, hatırda kalsın yeter! Tüm hız problemlerini çözecek olan bu denkleme ne kadar iltifat etsek azdır. Bu esitliği bilip de çözemeyeceğimiz hız problemi yoktur, inanmayan varsa sabretsin!.

Simdi ufak ufak soru-çözümlere başlayabiliriz:

Soru:

6x metrelik bir yolu, 3t dakikada giden bir hareket linin hızını bulunuz.

Çözüm:

Bulmamız gereken hıza V diyelim.

Yol = Hız × Zaman

olduğundan

6x = V.3t olur.

Denklemden V’yi çekersek;

olarak bulunur.

Hızın birimi çok önemlidir. Bu soruda uzaklık metre, süre de dakika cinsinden verildiğinden hızın birimini m/dk olarak yazdık. Başka birimler verseydi, hızın birimi de ona göre değişirdi.

Bazen hızın birimini özellikle soruda verilen birimler dışında sorarlar. Birimler arasındaki geçişleri yapmayı iyi bilmeliyiz. Hemen bunla ilgili bir soru çözelim o zaman.

Soru:

5 saniyede 60 metre giden bir trenin hızı kaç km/s’tir?

Çözüm:

Dikkat ettiyseniz soruda verilen süre saniye, yol metre cinsinden ama trenin hızı kilometre ve saat cinsinden soruluyor. Saniyeyi saate, metreyi kilometreye çevirmeyi bilen için çocuk oyuncağı gibi bir şey. Bilmeyene öğretelim.

Unutana da hatırlatalım:

1 saat = 60 dakika = 3600 saniye ve 1 kilometre = 1000 metre.

Trenimiz 5 saniyede 60 metre gidiyormuş.

Bize 1 saatte yani 3600 saniyede gittiği yol lazım. Bir orantı kurun, doğru olsun, cevap 43200 metre çıkacaktır.

E, bu da 43,2 km demektir. O halde trenin hızı 43,2 km/s’tir.

Soru:

Bir araç 100 km.lik mesafeyi sabit bir hızla 5 saatte almaktadır.

Bu aracın hızını m/dk cinsinden bulunuz.

Yanıt: 1000/3

Soru:

300 metre uzunluğundaki bir tren, 200 metre uzunluğundaki bir tüneli sabit bir hızla 40 saniyede geçmiştir. Bu trenin hızı kaç m/dk.dır?

Çözüm:

Bir trenin ilk vagonu tünelin içine girdiği anda, tren tünele girdi sayılır ama ilk vagon tünelden çıktığı anda tren tüneli geçti diyemeyiz. Allah göstermesin, o an tünelin yıkıldığını düşünün bakalım, tren tüneli geçmiş olsa hiç altında kalır mıydı? Demek ki tren hem kendi boyu kadar hem de tünel boyu kadar ilerlemeli.

x = V.t olduğundan 300 + 200 = V.40 olur.

Burada uzunluk metre, süre saniye olduğundan

V = 12,5 m/sn olur.

1 saniyede 12,5 metre gidiyorsa 60 saniyede yani 1 dakikada 750 metre gider.

O halde

V = 750 m/dk’dır.

Bu tarz sorularda tren bazen tüneli değil de elektrik direğini filan geçer. Bu tip sorularda elektrik direğini kalınlık sız düşüneceğiz. Yani öyle olmasa da bunları ihmal edeceğiz.

Soru:

200 mt. uzunluğundaki bir tren, 300 mt. Uzunluğundaki bir tüneli sabit bir hızla 50 saniyede geçmiştir.

Bu trenin hızı kaç m/dk’dır?

Yanıt: 600

Soru:

Her gün 6 saatte aldığı yolu, hızını 10 km/s arttırarak 5 saatte alan bir otobüsün eski hızı kaç km/s’tir? Ayrıca üşenmezseniz bu yolun uzunluğunu bulunuz.

Çözüm:

Otobüsün erken varma sebebi yolun kısalması değil, hızın artması. Yani dünkü yol, bugün de aynı yol. O zaman hem eski hızına göre, hem de yeni hızına göre

x = V.t denklemlerimizi kuralım.

Eski hızına V, yeni hızına V + 10 diyelim.

x = V.6 ve x = (V + 10).5

denklemleri eşitlenirse 6V = 5(V + 10) çıkar ki, buradan V = 50 bulunur.

5lk sorunun cevabını bulmuş olduk.

Simdi bunu canımızın istediği eşitlikte yerine yazalım:

x = 6.V = 6.50 = 300 km’dir.

Soru:

Her gün belli bir yolu belli bir sürede alan hareketli, hızını 20 m/dk arttırınca bu yolu 2 dakika erken, 10 m/dk azaltınca 4 dakika geç kalıyorsa, bu yol kaç metredir?

Çözüm:

Her günkü hızı V m/dk, her gün bu yolda geçen süre de t dakika olsun.

Hızını arttırsa da azaltsa da yola bir sey olduğu yok.

Yol ne azalır, ne kısalır.

Hemen x = Vt eşitliğini kuralım:

x = Vt = (V + 20)(t – 2) = (V – 10)(t + 4)

olur.

Parantezler açılırsa

x = Vt

x = Vt – 2V + 20t – 40

x = Vt + 4V – 10t – 40

çıkar.

–2V + 20t = 4V – 10t olduğundan

6V = 30t

yani V = 5t olur.

Simdi nerde V görürseniz gidin yerine 5t yazın.

x = 5t.t = (5t + 20)(t – 2) = (5t – 10)(t + 4)

olur.

Ben sizin yerinize t’yi buldum, t = 4 çıktı.

x = 5t² = 516 = 80 metredir.

4 saatte aldığı yolu, 3 saatte almak için hızını 10

km/s arttırmak zorunda olan hareketli var.

Yolun uzunluğu kaç km.dir?

Yanıt: 120

Aksilikler Olursa:

Bazen arabanın durduk yere arızalanacağı tutar. Veya adamın yolda mola veresi gelir. Veya hava koşullarından ötürü uçak rötar yapar.

Aksilik bu ya! Tam da gelir bizim sorumuzu bulur. Bu aksiliklerden doğan gecikmeler veya gecikmemek için hız arttırmalar, hız problemlerine çokça malzeme olur. Bu aksilikler o kadar önemli değil ama soruyu çözmenizde aksilik doğurursa o kötü! Mümkün olduğunca bol örnekle açıklamaya gayret edeceğim.

Başlıyoruz:

Soru:

900 kilometrelik (İstanbul-Adana arasını normal şartlarda 55 dakikada giden bir uçak hava muhalefeti nedeniyle (istanbul’dan 5 dakika rötarlı kalkmıştır. Uçağın (o sırada güllük gülistanlık olan) Adana’ya planlanan sürede varabilmesi için hızı kaç km/s olmalıdır?

Çözüm:

Rötarı telafi etmek için, her zaman 55 dakikada aldığı mesafeyi, o gün 50 dakikada almak zorundadır.

50 dakikada 900 kilometre gidiyorsa 60 dakikada yani 1 saatte 1080 kilometre gider. O halde uçağın hızı 1080 km/s olmalıdır.

Soru:

Saatteki hızı 60 km. olan bir kamyon A kentinden B kentine doğru harekete başladıktan 1 saat sonra, hızı 75 km/s olan bir otobüs, otobüsten 1 saat sonra da bir otomobil A’dan B’ye dogru harekete başlıyorlar.

Üçü aynı anda B’ye vardığına göre AB yolu kaç km.dir? Ayrıca otomobilin hızı kaç km/s’tir?

Çözüm:

Kamyon, otobüse göre 1 saat, otomobile göre 2 saat fazla seyahat etmistir. Yani, otomobil t saatte B’ye vardıysa, otobüs (t + 1), kamyon ise (t + 2) saatte varmıştır. Hepsinin aldığı yolun aynı olduğunu yine unutmuyoruz.

Otomobilin hızına V km/s diyelim.

x = 60(t + 2) = 75(t + 1) = V.t

denklemlerini çözersek t = 3 saat buluruz.

Bu yüzden x = 300 km. çıkar. Yine bu yüzden de

V = 100 km/s çıkar.

Soru:

A kentinden B kentine doğru saatte 40 km.lik hız yapan bir araç harekete baslıyor.

Bu araçtan 1 saat sonra aynı yerden aynı yönde doğru bir başka araç daha hareket ediyor. (kinci araç 1 saat geç çıkmasına rağmen B’ye ilk araçtan 1 saat erken varıyor.

AB yolu 480 km. ise ikinci aracın saatteki hızı kaç km/s’tir?

Çözüm:

Demek ki ikinci araç bu yolu birinci araçtan 2 saat daha az zamanda alabiliyor.

480 km.lik yolu ilk araç hızı 40 km/s olduğundan 1 saatte alır, o halde ikinci aracın bu yolu bitirmesi için gereken süre 10 saattir.

Sonuç olarak, ikinci aracın hızı 480/10 = 48 km/s olur.

Soru:

A kentinden B kentine doğru 60 km/s hızla bir araç harekete başlıyor.  Bundan 1 saat sonra hızı 75 km/s olan bir araç hareket ediyor.

İki araç B’ye aynı anda vardığına göre AB yolu kaç km.dir?

Yanıt: 300

Soru:

Saatteki hızı V km. olan bir araç belli bir yolu hep 10 saatte alıyor. Eğer yolun 1/3’ünü 2V hızla giderse, gelenek bozulmasın diye yolun kalanını hangi hızla gitmelidir?

Çözüm:

Yola, üçe kolay bölünsün diye 3x diyelim.

3x = V.10 olduğunu unutmayın. 3x’in x’ini 2V

hızla t saatte almıssa x = 2V.t olur.

O halde 3x = 6Vt, diğer yandan 3x = V.10 idi.

Buradan t = 5/3 bulunur.

Gelenek bozulmasındiye kalan 2x’lik yolu 10 – 5/3 = 25/3 saatte almalıdır.

Buradaki hızına da V₂ diyelim.

2x = V₂.25/3 olur. x yerine 10V/3 yazılırsa

V₂ = 4V/5 olarak bulunur.

Soru:

300 kilometrelik bir yolu, arabasıyla 6 saatte almayı planlayan bir adam, seyahate herhangi bir sebeple 1 saat geç baslamıstır.

Planlanan sürede gitmek istediği yere varabilmesi için hızını yüzde kaç arttırmalıdır?

Yanıt: 20

Soru:

Hızları saatte V₁, V₁ + V₂ ve V₁ – V₂ olan üç hareketliden birincinin 4t saatte aldığı yol A, ikincinin 3t saatte aldığı yol B ise üçüncünün t saatte aldığı yol A ve B cinsinden nedir?

Çözüm:

Üç hareketlinin de hızları da, bitirme süreleri de, yolları da farklı.

O zaman her biri için ayrı ayrı denklem yazalım.

Sorulana X diyelim.

A = V₁4t = 4V₁t

B = (V₁ + V₂)3t = 3V₁t +3V₂t

X = (V₁ – V₂)t = V₁t – V₂t

olduğundan ilk denklemden V₁t’yi A cinsinden çeker, onu ikinci denklemde yerine yazarak V₂t’yi de B cinsinden buluruz, böylelikle soru çözülmüş olur.

Soru:

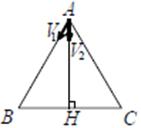Eskenar olan ABC üçgeni seklindeki bir pistin A kösesinden V₁ hızlı ve V₂ hızlı iki hareketli aynı anda harekete baslıyor.

V₂ hızlı olan AH yüksekliğinden gidip A’ya dönene kadar V₁ hızlı hareketli çevreyi dolasıp A’ya dönüyor.

Buna göre V₁/V₂ oranı kaçtır?

Çözüm:

Eskenar üçgenin bir kenarı 2 birim olsun.

Çevreyi dolasan V₁ hızlı hareketli 6 birim giderken, yükseklikten gidip gelen V₂ hızlı hareketli

birim yol alır.

Bu yolları alırken geçirdikleri süre aynı olduğundan hızları oranı aldıkları yollar oranıdır.

O halde ’tür.

Karşılaşma Problemleri:

İki hareketli aynı yolda birbirlerine doğru hareket ederlerse elbet bir zaman sonra karsılasacaklardır. Genel olarak 4 veri böyle sorulara yeter.

Bunlar: Birinci hareketlinin hızı, ikinci hareketlinin hızı, başlangıçta aralarındaki uzaklık ve karsılasmaları için geçmesi gereken süre.

Bu 4 veriden 3’ünü vererek dördüncü veriyi sorarlar.

Konunun ilk bölümündeki x = Vt

eşitliğini iyi anlamış biri için bu tarz sorular da bir oyuncak olacaktır.

Önce bir karsılaşma sorusu çözelim, ardından çözümü genelleyebilirsek genelleyeceğiz.

Soru: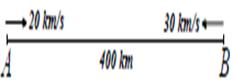

A ile B kentleri arası 400 km. olup A’dan saatteki hızı 20 km, B’den saatteki hızı 30 km. olan bir araç aynı anda birbirlerine doğru harekete başlıyorlar.

Kaç saat sonra karsılaşırlar?

Çözüm:

Tüm problem soruları gibi hemen sorulana adlandıralım. t saat sonra karşılaşsınlar.

t saatte yavaş olan 20t, hızlı olan 30t km yol alır.

Karsılastıklarına göre aldıkları yolların toplamı tam

400 km olmalı.

50t = 400 olduğundan t = 8 çıkar.

 

Simdi aynı mantıkla karsılaşma problemlerinin formülünü çıkartalım:

Yine karsılasmaları için geçmesi gereken süreye t saat diyelim.

A’dan kalkan t saatte V₁t, B’den kalkan t saatte V₂t km. yol alır.

Karsılasmaları için katettikleri toplam yol x km. olmalıdır.

x = V₁t + V₂t = (V₁ + V₂)t

Demek ki karsılaşma problemlerini hızlı çözebilmek için; iki aracın toplamına denk sadece tek bir araç varmış gibi düşüneceğiz.

Yol ve süre değişmez ama yeni aracımızın hızı V₁ + V₂ olacak

Soru:

Toprakta 20 km/s, asfaltta 40 km/s hızla gitmeye ayarlanmış iki farklı araç aralarındaki uzaklığın 800 km. olduğu A ve B kentlerinden birbirlerine doğru harekete başlıyorlar.

Yolun yarısı asfalt yarısı toprak ise bu iki araç kaç saat sonra karsılaşırlar?

Çözüm:

Bu soruyu normal karsılaşma problemi gibi düşünemeyiz. Çünkü asfaltta hareket eden daha hızlı olduğundan yolun ortasına daha önce gelir ve burada hızı değişmek zorundadır. Dolayısıyla hızı değişene kadar ne kadar süre geçtiğini önce bir bulalım bakalım.

Üst seklideki gibi, yolun ortası C, AC yolu toprak, CB yolu da asfalt olsun.

Asfaltta hareket edenin hızı 40 km/s ve asfalt 400 km. olduğundan 10 saatte hızlı olan yolun ortasına varır. Bu 10 saatlik sürede de A’dan kalkan 200 km. ilerlemiş ve AC’nin ortasına gelmiştir. Karsılaşmaları için toplam 200 km. gitmeleri lazım yani. Artık B’den kalkanın da hızının 20 km/s olduğunu unutmayın.

x = (V₁ + V₂)t olduğundan 200 = (20 + 20)t olur ki t = 5 bulunur.

Önceden de 10 saat geçmisti, o halde karsılasma ilk ana göre 15 saat sonra olur.

Soru:

Adana-İstanbul arası hala 900 kilometre. Adana’dan hızı 40 km/s olan bir kamyon ile İstanbul’dan hızı 35 km/s olan bir otobüs aynı anda birbirlerine doğru harekete başlıyorlar.

Bunlarla aynı anda da Adana’dan acayip bir sinek saatte 200 km.lik bir hızla (istanbul’a doğru uçmaya baslıyor.

Sinek, otobüsün camına değdiği anda durmadan aynı hızla geri dönüyor, bu sefer kamyon ile karsılasıyor ve onun camına değdiği anda yine aynı hızla durmadan geri dönüyor ve bu böyle devam ediyor.

Kamyon ile otobüs sonunda çarpışıyor ve sineğimiz vefat ediyor. Allah rahmet etsin ama sinek ölmeden önce kaç km. yol katetmistir?

Çözüm:

Hiç gülme, süper bir karsılaşma sorusudur!

Sineğin hızı belli değil mi? Belli. O halde kaç saat uçtuğunu bulursak, soruyu çözmüş olacağız. Kaç saat uçtu? Bu iki aracın harekete başlamalarından çarpı-sana kadar geçen süre kadar.

E, 900 km.lik  bir mesafede hızları 40 ve 35 km/s olan iki araç 900/(40 + 35) = 12 saat sonra karsılasırlar…

Demek ki rahmetlik 12 saat uçtu.

Bundan dolayı 200.12 = 2400 km. yol katetmistir.

Peki, aynı anda aynı yerden aynı yöne doğru harekete baslayan iki araç karşılaşabilir mi? Karşılaşamaz değil mi?Siz öyle zannedin!

Soru:

A ve B kentleri arası 200 km. olup, A’dan aynı anda iki araç aynı yöne doğru birlikte harekete başlıyorlar. Birinin hızı 20 km/s, diğerinin ise 30 km/s olsun. Hızlı olan B’ye vardığında durmadan geri dönüyorsa, bu iki araç ilk hareketten kaç saat sonra karsılaşırlar?

Ayrıca karsılaşma yerinin A’ya olan uzaklığı kaç km.dir?

Çözüm:

Gördünüz değil mi, karsılasabilirlermis!

Simdi bu soruya iki farklı çözüm sunacağız.

Birinci yol.

Hızlı olan B’den döndükten sonra AB arasındaki bir C noktasında karsılastıklarını farzedelim.

|BC| = x ise |AC| = 200 – x olur.

Yollar belli, hızlar belli, süreler de aynı, e ne duruyoruz?

200 – x = 20.t

200 + x = 30.t

olduğundan

400 = 50.t olur ki buradan t = 8 çıkar.

O halde A’dan kalkan 8 saatte 20.8 = 160 km. yol almıstır.

İkinci yol.

Karsılastıkları anda ikisinin aldıkları yolun toplamı 400 km. olmaz mı?

E, hızları toplamı da 50 km/s, o zaman dogal olarak t = 8 çıkar.

Yetişme Problemleri:

Tavşan-kaplumbağa hikayesini bilirsiniz.

Tavşan, kaplumbağaya hep ‘’Sen önden basla!’’ der. Niye? Kendi çok hızlı ya, nasıl olsa ona yetisirim diye… Tabi, bu sigara içmeyen bir tavşan! Kazın ayağı hep öyle olmasa da genelde doğrudur. Hızlı olan yavaştan daha geride yarışa başlasa bile eğer yeterli mesafe ve nefes veya benzin varsa hızlı yavaşsa yetişir.

Simdi böyle problemlere örnekler vereceğiz. Eğer yine becerebilirsek, yetişme problemlerinin de formülünü çıkartacağız

Soru:

Hızı 30 km/s olan bir hareketli, hızı 20 km/s olan baska bir hareketliden 50 metre önde harekete baslarsa, arkadaki öndekine kaç saat sonra yetisir?

Ayrıca hazır bunları bulmusken nerede yakalayacağını da bulunuz.

Çözüm:

Yine iki türlü çözüm yapacağız.

Tabii inat eden 10 farklı çözüm de bulabilir.

Birinci yol.

Arkadaki öncekini t saat sonra Y’de yakalıyor olsun.

Aynı üst resimde çizdiğimiz gibi.

BY yoluna y diyelim. Yavaş hareketli y km, hızlı ise

50 + y km. yol almıstır.

Her biri için denklemlerimizi kuralım:

y = 20.t

50 + y = 30.t

esitliklerinden ilkini ikincisinde yerine yazarsak t = 5 çıkar, ayrıca y = 100 çıktığında hızlı araç, yavaşı

B’den 100 km. ilerde yakalarmıs.

İkinci yol.

Yavaş saatte 20 km, hızlı ise 30 km. yol alıyor.

Demek ki hızlı olan her 1 saatte 10 km. yavaşsa yaklaşıyor.

Yetişmesi için 50 km. yaklaşmalı.

1 saatte 10 km. gidiyorsa

? saatte 50 km. gider?

doğru orantısını kurarsak, t = 5 bulunur.

Gerisi aynı ilk yolu çözdüğümüz gibi.

Simdi bu yaptıklarımızı genellemeye çalışalım.

Bakalım ne çıkacak?

Geriden başlayanın hızı V₁ km/s, önde başlayanın hızı V₂ km/s, aradaki fark da x km. olsun.

Hem kaç t saat sonra yetişeceğini, hem de B’den kaç km. ilerde yakalayacağını yani y’yi bulalım.

Nasıl mı bulalım?

İkinci yol daha güzel ama biz, eski tas  eski tarak, ilk yoldan gidelim.

Gidelim ki, ‘’Hala ben x = V.t denklemini kuramıyorum!’’ diyen kalmasın…

Arkadan kovalayan için: x + y = V₁.t

Önde kaçan için:

y = V₂.t

Bu iki denklemden (çıkarma yapılırsa);

bulunur ki, bunlar da yetime problemlerinin formülüdür.

Biraz da gidilen yolun dairesel olduğu durumlara bakalım.

Genel itibariyle ögrenciler, dairesel pist kelimesini veya seklini gördüler mi, soruyu yapamıyorlar.

Ben de bunu bir türlü anlayamıyorum.

Sanki hayatta her gün yürüdükleri yollar  cetvelle çizilmiş!

Dairesel pist sorularında çember bilgisi gerektiğini zannediyorlar herhalde. Öyle olsa gerek.

Evet, bazen gerekir ama ilkokul 4 veya 5’te öğretilen ‘’Yarıçapı r olan bir çemberin çevresi ’dir’’ bilgisi yeter.

Bir de ‘’Bir daire diliminin merkez veya yay açısının ölçüsü 360’ın kaçta kaçıysa daire dilimi veya yay uzunluğu da dairenin o kadarda o kadarıdır.’’ bilgisi kullanılır. Buna rağmen ‘’Ben gördüm hocam, başka bilgilerin de bilinmesi gereken dairesel pist soruları var!’’ diyorsan hala, ne diyeyim, git ‘’çember ve daire’’ konusunu çalıs o zaman! Hem hangi matematik konusunda bir başka konuya ait bilgiler kullanılmıyor ki?

Soru:

O merkezli dairesel bir pistin A ve B noktalarından şekilde görüldüğü üzere iki hareketli aynı anda aynı yöne doğru harekete başlıyorlar.

Yavaşın hızı 12 m/dk hızlının hızı 16 m/dk olduğuna göre, hızlı yavaşa ilk kez nerde yetişir?

Ayrıca (bulunabilirse eğer) AB yolunun boyunu bulunuz.

 

Çözüm:

Yine iki yoldan çözelim.

Birinci yol.

AB uzunluğuna x diyelim. Formülümüz gereği x = (16 – 12).t = 4t olur. Bu da x’i bulmak için t’nin bilinmesi gerektiğini anlatır.

Demek ki x bulunamaz. Yani AB yolu bu verilerle bulunamaz.

Nerde yakalar sorusuna cevap arayalım. Yani y’yi bulalım.

Yine formülümüze başvuralım:

olduğundan hızlı yavaşı B’den 3x metre sonra yani A’da yakalar.

İkinci yol.

Hızların 12 ve 16 m/dk olması bize yavaşın her 3 birim yol aldığında, hızlının 4 birim yol alması gerektiğini anlatır.

O halde yavaş 3 çeyrek çember yayı giderse, hızlı 4 çeyrek çember yayı gider ki bu da A’da yakalaması demek olur.

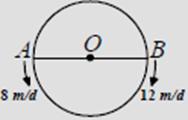O merkezli dairesel pistin çevresi 96 metredir.

AB çapının uç noktalarından şekildeki gibi saatteki hızları 8 ve 12 m/d olan iki bisikletli aynı anda birbirlerine doğru harekete başlıyorlar.

İlk kez kaç dakika sonra karşılaşırlar?

Yanıt: 1,2

Ortalama Hız:

100 kilometrelik bir yolu bir araçla 2 saatte gittiğinizi düşün. Sizce bu seyahatteki aracın hızı kaç km/s idi? 50 km/s diyorsun değil mi?

Simdi bu 50 sayısı üstüne biraz düşünelim bakalım. Ne demek bu 50?

Birileri bir aracı hep 50 km/s hızla gitmeye ayarlamış, sen de bu araca, önünden geçerken, kapısını açıp içine atlamışsın, 100 kilometre ilerde de aşağı atlamışsın!

Bu mu yani?

Elbet bu değil! Araç bazen durmuş, bazen hızlanmış, bazen yavaşlamış, sonuçta 100 kilometreyi bitirdiğinde tam 2 saatin geçtiğini görmüşsün.

Onun için de diyorsun ki elliyle geldik.

Anlayacağınız, bu aracın hangi an, hangi yerde, hangi hızı yaptığını bulmak mümkün olmadığından, ‘’bu aracın hızı 50 km/s’tir’’ dediğimizde kullandığımız hız kelimesi ortalama hız manasındadır.

Değilse de böyle olmalıdır.

Toplam yolu, toplam zamana bölersek bulacağımız şey ortalama hızdır.

Yani, birotobüs Adana’dan

İstanbul’a 10 saatte gitmişse ortalama 90 km/s hızla gitmiştir diye düşünmeliyiz.

‘’Adana – İstanbul arasının kaç kilometre olduğunu vermemişsin ki!’’ diyorsan, ben de sana notları neden en basından itibaren okumadığını sorarım.

Ortalama hız, yoldan bağımsızdır.

Yani, buradan İstanbul’a da 20 km/s hızla gidip geriye 30 km/s hızla dönsen, arka mahalleye de 20 km/s hızla gidip, geriye 30 km/s hızla dönsen ortalama hızın aynı ve 24 km/s çıkar. Bunu ilerde ilk örnekte kanıtlayacağız.

Ortalama hızı bulmanın bir başka yolu da, yine kanıtını ilk örneğe bakarak siz yapınız, gidilen ve dönülen hızların harmonik ortalamasını bulmaktır.

Yani, A’dan B’ye V1 km/s hızla gidip, B’ den A’ya V₂ km/s hızla dönen bir aracın bu seyahatteki ortalama hızı,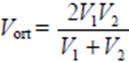

formülüyle bulunabilir.

Ortalama hız, her zaman en fazla süre ayrılan hıza diğerlerine göre daha yakındır. Eğer bir yerden bir yere iki değişik hızla gidilmiş ve her ikisine de eşit süre ayrılmışsa, ortalama hız bu iki hızın toplamının yarısı yani aritmetik ortalamasıdır.

Eğer bu iki hızdan birisiyle daha çok seyahat etmişsen ortalama hızın kesinlikle bu iki hızın aritmetik ortasından daha çok süre gidilen hıza yakındır.

Örneklerle daha iyi anlayacaksın.

Soru:

A kentinden B kentine 20 km/s hızla gidip, geriye 30 km/s hızla dönen bir aracın bu seyahatteki ortalama hızı kaç km/s’tir?

Çözüm:

Gidişte ve dönüşte yol değişmediğinden geçen süre hızlarla ters orantılıdır.

Yani gidiş dönüş hızlarının oranı 2/3 olduğundan gidiş-dönüş sürelerinin oranı 3/2’dir. Bundan dolayı giderken 2t saat süre geçmişse, dönerken 3t saat süre geçer diyebiliriz.

Ortalama hız neye eşitti? Toplam yolun, toplam zamana oranına.

Yolumuz 203t veya 30.2t çarpımlarından 60t olur.

Toplam yol o zaman, gidip dönüldüğü için 120.t yapar, toplam zaman da 5.t olduğundan

V_ort = 120t/5t = 24 km/s’tir.

Dikkat ettiyseniz yolun uzunluğunu bilmemize rağmen cevap 24 çıktı, bu da ortalama hızın yoldan bağımsız olduğuna kanıttır.

Soruyu bir de harmonik ortalama formülü ile çözelim:

Soru:

Bir araç gideceği yolun 1/3’ünü 20 km/s hızla, kalanını da 50 km/s hızla gitmiştir. Bu aracın bu seyahatteki ortalama hızını bulunuz.

Çözüm:

Madem ortalama hız yoldan bağımsız, yani yol kaç birim olursa olsun bir şey değişmiyor, en küçük yola hem 20’ye hem de 50’ye bölünebilen bir sayı verelim.

Hızını değiştirdiği yer K olsun.

|AK| = 100 km. ve

|KB| = 200 km. olsun.

|AK|’yı o halde 5 saatte,

|KB|’yi 4 saatte alır.

Toplam yolu toplam zamana

Bölelim

V_ort = 300/9 = 100/3 km/s olur.

Soru:

A kentinden B kentine 10 km/s sabit hızla gidip, 15 km/s sabit hızla dönen bir aracın bu seyahatteki ortalama hızı kaç km/s’dir?

Yanıt: 12

Soru:

Yine geriden başlayanın hızı V1 km/s, önde başlayanın hızı V2 km/s, aradaki fark x km. ve bu şartlar altında, arkadaki öndekini B’den y km. ilerde yakalıyor olsun.

Eğer araçlar hızlarını 4 katına çıkarırlarsa, arkadakinin öndekini yakaladığı yer, B’den kaç y ilerde olur?

Çözüm:

İnanmayacaksın ama değişmez!.

Değişen sadece yetişme süresi olur.

Önceden t saat sonra yakalıyorsa, simdi hızı 4 katına çıktığından t/4 saat sonra yakalar.

İki aracın arasındaki mesafe değişmediği ve hızları aynı oranda arttığı sürece bunu hep yapabiliriz. Siz yine de matematiksel kanıtını yapmaya çalısın.

Dediğime geleceksiniz.

Hız problemleri hakkında artık az çok bilgi edindiniz sayılır.

Birkaç örnek daha çözüp, sizi o çok sevdiğiniz alıştırma soruları ile bas basa bırakacağım, sabırsızlanmayın!

Soru:

A’da ve B’de duran iki araç eğer aynı anda birbirlerine doğru hareket ederlerse, K’da karşılıyorlar.

Hızlarını değiştirmeden aynı anda aynı yöne doğru hareket ederlerse, arkadaki öndekine

Y’de yetişiyor.

|AB| = 3x, |BC| = 2x ve |BY| = x + 10 birim uzunluğunda ise x kaçtır?

Çözüm:

Önce karsılaşma durumunu inceleyelim.

Aynı anda kalktılar, aynı anda K’ya vardılar.

Yani K’ya geliş süreleri eşit. Peki, biri niye diğerine göre daha çok yol aldı?

Daha hızlı olduğundan. Peki, ne kadar hızlı olduğunu nerden bulacağız?

Gittikleri yol oranından. Demek ki, bu araçların hızları oranı 2/3’müş.

Hızlarını değiştirmeden aynı yöne giderlerse, hızlı olan yavaşa Y’de yetiyormuş.

Bu ne demek? B’den kalkan yani yavaş olan

x + 10 birim yol alana dek, A’dan kalkan yani hızlı olan

6x + 10 yol alıyormuş.

Yine süre aynı olduğundan, hızlar oranı gittikleri yolların oranını verir.

O halde;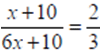

orantısı çözülürse x = 10/9 olarak bulunur.

Soru:

Bir araç, beli bir yolu V km/s hızla hep t saatte almaktadır. Eğer hızını %50 arttırır, bu yolu da %40 azaltırsak, simdi kaç t saatte alır?

Çözüm:

Bence süredeki değişmeyi kolay gözlemlemek için ilk süre 100 saat olacak şekilde bir ayarlama yapalım. Yol 200 km. olsun, hızı da 2 km/s. Hız %50 artarsa 3 km/s, yol %40 azalırsa 120 km. olur.

120 = 3.t_y eşitlginden t_y = 40 olur.

O halde, 100 iken 40’a düşen, t iken (2/5)_t’ye düşer.

Siz başka sayılarla yapsaydınız da aynı çıkardı.

Hatta hiç böyle sayı vererek değil de x = V.t üzerinde oynamalar yapsaydınız da!.

Lütfen bir de öyle çözünüz.

Soru:

Bir adamın nefesi, durmadan yüzmeye en çok 15 dakika yetmektedir.

Kıyıdan denize doğru açılmak isteyen adam kıyıya vuran dalgalara karsı dakikada 8 metre, dalgalarla birlikte dakikada 12 metre hızla yüzüyorsa, en çok kaç metre kıyıdan açılabilir?

Çözüm:

Kıyıdan açıldığı mesafe, giderken ve dönerken değişmeyeceğinden, gidip ve dönüş sürelerinin oranını, gidiş ve dönüş hızlarının oranından bulabiliriz.

Hız oranı 8/12 = 2/3 olduğundan geçen süre oranı 3/2 olmalıdır.

Yani, 3t dakika açılmış, 2t dakikada kıyıya geri dönmüş bu şahsiyet.

Soruda 3t + 2t = 15 dk. verilmiş, o halde t = 3 dk, dolayısıyla

x = 8.3t veya x = 12.2t eşitliklerinden

adamın en çok

x = 72 metre açılabileceği bulunur.

 

Burada bulunan Matematik Hız ve Hareket Problemleri Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]