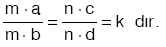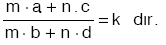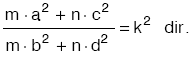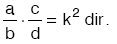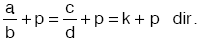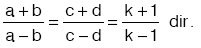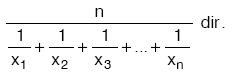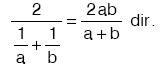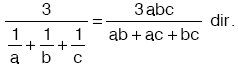ORAN ORANTI Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik ORAN ORANTI online ders anlatımı yapan gözde hocaların ORAN ORANTI konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik ORAN ORANTI video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik ORAN ORANTI konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik ORAN ORANTI konusu ile ilgili yazılı anlatım ve genel ORAN ORANTI formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik ORAN ORANTI Konu Anlatımı Videolar
Matematik ORAN ORANTI Konu Anlatımı 2 Şenol Hoca
Matematik ORAN ORANTI Konu Anlatımı 3 Şenol Hoca
Matematik ORAN ORANTI Konu Anlatımı 2 TeknoFem
Matematik ORAN ORANTI Konu Anlatımı 3 TeknoFem
Matematik ORAN ORANTI Konu Anlatımı 2 (Doğru Orantı) Hocalara Geldik
Matematik ORAN ORANTI Konu Anlatımı 3 (Ters Orantı) Hocalara Geldik
Matematik ORAN ORANTI Konu Anlatımı 4 (Bileşik Orantı) Hocalara Geldik
Matematik ORAN ORANTI Konu Anlatımı 5 (Aritmetik Ortalama) Hocalara Geldik
Matematik ORAN ORANTI Konu Anlatımı 6 (Geometrik ve Harmonik Ortalama) Hocalara Geldik
Matematik ORAN ORANTI Konu Anlatımı 2 (BİLEŞIK ORANTI METODU)) Tonguc Akademi
Matematik ORAN ORANTI Konu Anlatımı 2 MatAkademi
[t2]
Sitemizde Aşağıda yer alan Matematik ORAN ORANTI Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik ORAN ORANTI canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.
Matematik ORAN ORANTI Konu Anlatımı Yazıl
A. ORAN
a ve b reel sayılarının en az biri sıfırdan farklı olmak üzere, 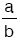 ye a nın b ye oranı denir.
ye a nın b ye oranı denir.
| • Oranlanan çokluklardan ikisi aynı anda sıfır olamaz.• Oranın payı ya da paydası sıfır olabilir.• Oranlanan çoklukların birimleri aynı tür olmalıdır.• Oranın sonucu birimsizdir. |
B. ORANTI
En az iki oranın eşitliğine orantı denir. Yani 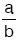 oranı ile
oranı ile 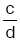 nin eşitliği olan
nin eşitliği olan 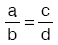 ye orantı denir.
ye orantı denir.
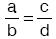 ise, a : c = b : d dir. Buradaa ile d ye dışlar, b ile c ye içler denir. ise, a : c = b : d dir. Buradaa ile d ye dışlar, b ile c ye içler denir. |
DOĞRU ORANTI NEDİR? İki çokluktan biri artarken diğeri de aynı oranda artıyorsa ya da biri azalırken diğeri de aynı oranda azalıyorsa bu çokluklar doğru orantılıdır. Doğru orantıya örnek verecek olursak:
► 1 kg portakal 3 TL ise 2 kg portakal 6 TL’dir. Burada ağırlık ile fiyat doğru orantılıdır.
► Benzer şekilde dakikada 1 soru çözen bir kişi aynı hızla 10 dakikada 10 soru çözer.
Burada şu göz ardı edilmemelidir: Çoklukların ikisi de aynı oranda artmalı veya azalmalıdır. Yani biri 2 katına çıktığında diğerinin de 2 katına çıkması gerek. Örneğin çocukken yaşımız arttıkça boyumuz uzar ama yaşımız 2 katına çıktığında boyumuz 2 katına çıkmaz. Burada doğru orantı yoktur.
TERS ORANTI NEDİR? İki çokluktan biri artarken diğeri de aynı oranda azalıyorsa ya da biri azalırken diğeri de aynı oranda artıyorsa bu çokluklar ters orantılıdır. Ters orantıya örnek verecek olursak:
► Bir duvarı 5 işçi 4 günde örüyorsa, 10 işçi 2 günde örer. İşçi sayısı arttığında (2 kat) işin bitme süresi de (yarıya) düşer. İşçi sayısıyla süre ters orantılıdır.
► Benzer şekilde 100 km/sa hızla 3 saatte gidilen bir yol 50 km/sa hızla 6 saatte gidilir. Hız düşünce yol daha uzun sürede biter.
C. ORANTININ ÖZELİKLERİ
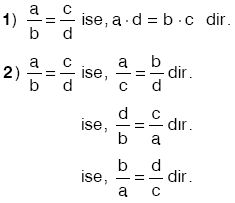
3) m ile n den en az biri sıfırdan farklı olmak üzere,
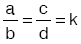 ise, (k ya orantı sabiti denir.)
ise, (k ya orantı sabiti denir.)
•
•
•
•
•
•
a : b : c = x : y : z ise,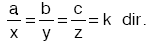 |
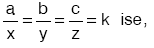 a = x × k, b = y × k, c = z × k, a = x × k, b = y × k, c = z × k,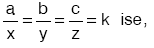 |
D. ORANTI ÇEŞİTLERİ
1. Doğru Orantılı Çokluklar
Orantılı iki çokluktan biri artarken diğeri de aynı oranda artıyorsa ya da biri azalırken diğeri de aynı oranda azalıyorsa bu iki çokluk doğru orantılıdır denir.
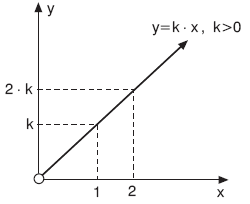
x ile y çoklukları doğru orantılı ve k pozitif bir doğru orantı sabiti olmak üzere, y = k × x ifadesine doğru orantının denklemi denir. Bu denklemin grafiği diğer sayfada verilmiştir.
x ile y çokluklarının doğru orantılı olduğu grafik aşağıdaki gibidir.
(x > 0 ve y > 0)
| • İşçi sayısı ile üretilen ürün miktarı doğru orantılıdır.• Bir aracın hızı ile aldığı yol doğru orantılıdır. |
2. Ters Orantılı Çokluklar
Orantılı iki çokluktan biri artarken diğeri aynı oranda azalıyorsa ya da biri azalırken diğeri aynı oranda artıyorsa bu iki çokluk ters orantılıdır denir.
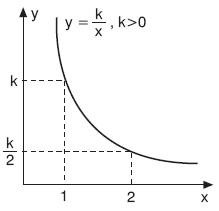
x ile y çoklukları ters orantılı ve k pozitif bir ters orantı sabiti olmak üzere, 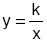 ifadesine ters orantının denklemi denir.
ifadesine ters orantının denklemi denir.
x ile y çokluklarının ters orantılı olduğu grafik aşağıdaki gibidir.
(x > 0, y > 0 ve k > 0)
| • İşçi sayısı ile işin bitirilme süresi ters orantılıdır.• Bir aracın belli bir yolu aldığı zaman ile aracın hızı ters orantılıdır. |
a, b ile doğru c ile ters orantılı ve k pozitif bir orantı sabiti olmak üzere,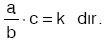 |
E. ARİTMETİK ORTALAMA
n tane sayının aritmetik ortalaması bu n sayının toplamının n ye bölümüdür.
Buna göre, x1, x2, x3, … , xn sayılarının aritmetik ortalaması, 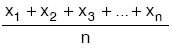 dir.
dir.
• a ile b nin aritmetik ortalaması
• a, b, c biçimindeki üç sayının aritmetik ortalaması,
• n tane sayının aritmetik ortalaması x olsun.
Bu n tane sayının herbiri; A ile çarpılır, B ilave edilirse oluşan yeni sayıların aritmetik ortalaması Ax + B olur.
F. GEOMETRİK ORTALAMA
n tane sayının geometrik ortalaması bu sayıların çarpımının n. dereceden köküdür.r.
Buna göre,
x1, x2, x, … , xn sayılarının geometrik ortalaması 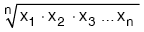 dir.
dir.
• a ile b nin geometrik ortalaması (orta orantılısı) 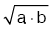 dir.
dir.
• a, b, c biçimindeki üç sayının geometrik ortalaması, 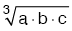 dir.
dir.
• a ile b nin aritmetik ortalaması geometrik ortalamasına eşit ise
a = b dir.
G. HARMONİK (AHENKLİ) ORTA
x1, x2, x3, … , xn sayılarının harmonik ortalaması
- a ile b nin harmonik ortalaması
- a, b, c gibi üç sayının harmonik ortalaması
- İki pozitif sayının aritmetik ortalaması A, geometrik ortalaması G ve harmonik ortalaması H ise,
i) G2 = A × H dır.
ii) H £ G £ A dır.
H. DÖRDÜNCÜ ORANTILI
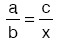 orantısını sağlayan x sayısına a, b, c sayıları ile dördüncü orantılı olan sayı denir.
orantısını sağlayan x sayısına a, b, c sayıları ile dördüncü orantılı olan sayı denir.
- Matematik ORAN ORANTI Çözümlü soruları izlemek ve ORAN ORANTI İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik ORAN ORANTI Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]