Matematik Sayılar Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Sayılar online ders anlatımı yapan gözde hocaların Sayılar konu anlatımı videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Sayılar video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Sayılar konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Sayılar konusu ile ilgili yazılı anlatım ve genel Sayılar formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)
Eğitim-Dünyası.net olarak iyi dersler dileriz
Doğal sayılarda dört işlem Ekol Hoca
DOĞAL SAYILAR 2 (çözümleme) Şenol Hoca
TAM SAYILAR 1 (çift-tek ve pozitif-negatif)
TAM SAYILAR 2 (ardışık sayılar ve hızlı toplama)
TABAN ARİTMETİĞİ – Şenol Hoca
Sayı Basamakları (2/4) TeknoFem
Sayı Basamakları (3/4) TeknoFem
Sayı Basamakları (4/4) TeknoFem
TABAN ARİTMETİĞİ Fatih hoca
Taban Aritmetiği Konu Özeti İbrahim Hoca
Sayı Basamakları Konu Anlatımı MatAkademi
[t2]
Sitemizde Aşağıda yer alan Matematik Sayılar Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Sayılar canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.
Matematik SAYILAR Yazılı Konu Anlatım
SAYI SİSTEMLERİ:
A. SAYI BASAMAĞI:
4 bir basamaklı, 14 iki basamaklı, 345 üç basamaklı, 8716 dört basamaklı bir doğal sayıdır. Buna göre, bir doğal sayıda kaç tane rakam varsa sayı o kadar basamaklıdır.
B. Sayı Sistemleri (ÇÖZÜMLEME):
1) Sayı Değeri: Basitçe bir tanımla bir sayıyı oluşturan rakamlara o sayının sayı değeri denilmektedir.
Doğal sayıyı oluşturan rakamların bulunduğu yerdeki değerine basamak değeri denir.
Basamak değerlerinin toplamına o sayının çözümlenmiş biçimi denir.
Üç basamaklı abc sayısı aşağıda çözümlenmiştir.
- ab = 10 × a + b
- abc = 100 × a + 10 × b + c
- aaa = 111 × a
- ab + ba = 11 × (a + b)
- ab – ba = 9 × (a – b)
- abc – cba = 99 × (a – c)
- abcd = cd + 100 × ab = bcd + 1000 × a
6327 sayısının sayı değerleri toplamı nedir?
6+3+2+7=18
2) Basamak Değeri: Kpss matematik konuları içinde yer alan basamak değeri, bir sayıyı oluşturan rakamların bulunduğu konuma o rakamın basamak değeri denilmektedir.
2457 sayısını örnek verecek olursak. Buradaki 4, yüzler basamağında bulunduğu için 4’ün basamak değeri 4×100=400’dür. 5’in basamak değeri 5×10=50’dir. 2’nin basamak değeri de binler basamağında olduğundan 2×1000=2000 oalcaktır.
Doğal sayılar içinde bütün rakamların basamak değerlerini yazıp toplarsak doğal sayıyı çözümlemiş oluruz. Bu bakımdan basamak değeri bize bir sayının çözümlenmesini gösterir. Kpss sorularında da bu alanda sorulan sorular sayı çözümleme tarzındadır.
Sayı sistemleri içinde yer alan basamak değerleri abc tarzında sorularla da karşımıza çıkmaktadır.
abc= 100a+10b+c şeklinde çözümlenmektedir.
2a8b= 2000+100a+80+b şeklinde çözümlenir.
ab+ba = 10a+b+10b+a
= 11a+11b = 11(a+b)
ab-ba = 10+b-(10b+a)
= 10a+b-10b-a = 9a-9b
= 9 (a-b)
abc-cba = 100a+10b+c-(100c+10b+a)
= 100a+10b+c-100c-10b-a = 99a-99c
= 99(a-c)
Şimdi kpss genel yetenek matematik sorularında çıkan basamak değeri ile ilgili birkaç soru örneği çözelim.
abc ve cba üç basamaklı doğal sayılardır.
abc-cba = 693 olduğuna göre a+b+c toplamının alabileceği en büyük değer kaçtır?
abc-cba = 693
100a+10b+c-(100c+10b+a) = 693
100a+10b+c-100c-10b-a = 693 => 99a-99c = 693 olur. Buradan;
99 (a-c) = 693 => a-c= 7 olur.
a+b+c toplamının en büyük değeri için a=9, c=2 ve b=9 alınır. (Rakamları farklı demediği için aynı rakamları seçebiliriz.)
a+b+c=9+9+2= 20
İki basamaklı ab sayısı ile bu sayının rakamları yer değiştirilerek elde edilen iki basamaklı ba sayısının farkı 54 ise bu koşula uygun yazılabilecek ab sayılarının toplamı kaçtır?
ab-ba= 54
10a+b-(10b-a) = 54
10a+b-10b-a= 54
9 (a-b) =54 buradan a-b= 6 çıkar. Şimdi bu koşula uyan ab sayılarını bulalım;
a=9 iken b=3 ; 93
a=8 iken b=2 ; 82
a=7 iken b=1 ; 71 => elde edilen tüm ab sayılarını toplarsak;
93+82+71 = 246 sonucu çıkmaktadır.
C. TABAN
Bir sayının tanımladığı sayma sistemine sayının tabanı denir.
Z taban olmak üzere,
(abcd)z = a × Z3 + b × Z2 + c × Z + d dir.
Burada,
- Z, 1 den büyük ve doğal sayıdır.
- a, b, c, d rakamları Z den küçüktür.
- Taban belirtmeden kullandığımız sayılar 10 luk tabana göredir.
- (abc,de)T = a × Z2 + b × Z + c + d × Z–1 + e × Z–2 dir.
1. Onluk Tabanda Verilen Sayının Herhangi Bir Tabana Çevrilmesi
Onluk tabanda verilen sayı, hangi tabana çevrilmek isteniyorsa, o tabana bölünür. Bölüm tekrar tabana bölünür. Bu işleme bölüm 0 olana kadar devam edilir.
Ardışık olarak yapılan bu bölmelerden kalanlar sondan başlayarak (ilk kalan son rakam olacak şekilde) sıralanmasıyla istenen sayı oluşturulur.
2. Herhangi Bir Tabanda Verilen Sayının 10 luk Tabana Çevrilmesi
Herhangi bir tabandan 10 luk tabana geçirilirken verilen sayı, ait olduğu tabana göre çözümlenir.
3. Herhangi Bir Tabanda Verilen Sayının Başka Bir Tabanda Yazılması
Herhangi bir tabanda verilen sayı önce 10 tabanına çevrilir. Bulunan değer istenen tabana dönüştürülür.
4. Taban Aritmetiğinde Toplama, Çıkarma, Çarpma İşlemleri
Değişik tabanlarda yapılacak işlemler 10 luk sistemdekine benzer biçimde yapılır.
K tabanında verilen sayılarda toplama ve çarpma işlemleri bilinen cebirsel işlem gibi yapılır, ancak sonuç T den büyük çıkarsa içinden K ler atılıp kalan alınır. Atılan K adedi elde olarak bir sonraki basamağa ilave edilir.
Çıkarma işlemi yapılırken 10 luk sistemdekine benzer biçimde, bir soldaki basamaktan 1 (bir) almak gerektiğinde, bu 1 in aktarıldığı basamağa katkısı tabanın sayı değeri kadardır. Fakat alındığı basamaktaki rakam 1 azalır.

Faktöriyel
Faktöriyel, 1’den başlayarak n’ye kadar olan pozitif tam sayıların çarpımına denilmektedir. Bu çarpıma n faktöriyel denir ve n! şeklinde gösterilir. Kpss matematik dersinde yer alan bazı faktöriyel açılımları şu şekildedir:
0!=1
1!=1
2!=2.1=2
3!=3.2.1=6
4!=4.3.2.1=24
5!=5.4.3.2.1=120
6!=6.5.4.3.2.1=720
Kpss sorularında genelde 6! ve üstü direkt olarak sorulmaz. Sorular 6! ve daha düşük faktöryellere indirgenebilen sorulardır. Bize yüksek rakamlı faktöryel verildiği zaman emin olun ki yapılan işlemlerden sonra nihai olarak hesaplayacağımız faktöryel sonucu 6! üstünün geçmemektedir. Bu yüzden soruları hızlı çözebilmemiz açısından ufak olan faktöriyelleri ezberlememiz yerinde olacaktır.
Faktöriyel Özellikleri:
- Büyük faktöriyel kendisinden küçük olan herhangi bir faktöriyele indirgenebilir.
5!=5.4.3!
11!=11.10.9.8.7!
- Büyük faktöriyel, küçük faktöriyelin çarpanlarını içerisinde bulundurmaktadır. Bunun için küçük faktöriyeli tam bölen her sayı büyük faktöriyeli de kesinlikle tam böler.
6! i tam bölen herhangi bir sayı 6 faktöryelden sonra gelen herhangi bir faktöryeli de tam bölecektir. Yani 7! de 8! de ya da sonrasında gelen tüm faktöriyeller 6’ya tam bölünecektir. Çünkü içlerinde 6 çarpanı bulunmaktadır. 6 çarpanı varsa o sayı 6’ya tam bölünebilir demektir.
- 5! ve sonrasında gelen faktöriyellerin son basamağında kesinlikler 0 bulunur.
- 2! ve sonrasından gelen faktöriyellerin hepsi çift sayıdır.
Faktöriyel Soru Tipleri:
- ”Sondan kaç basamağı sıfırdır?” ya da ”Sondan kaç basamağı 9’dur?” gibi sorularda verilen faktöryel sayısı devamlı olarak 5’e bölünür.
80! – 1 sayısının sondan kaç basamağı 9’dur?
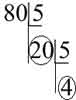
Burada 80’i devamlı olarak 5’e böldüğümüzde;
20+4= 24 çıkar. Dolayısıyla 80! sayısının sondan 24 basamağı 9’dur. Eğer bize ”Sondan kaç basamağı 0’dır?” diye sorulsaydı cevap yine 24 olacaktı. Basit bir örnekle 1000 sayısının sondan 3 basamağı 0’dır. 1000-1 sonucu da 999’dur ve 999’un son üç basmağı 9’dur ki bu zaten sayının tamamıdır. Kısaca sondan kaç basamağı 0’dır ya da sondan kaç basamağı 9’dur (x!-1 olarak verildiğinde) sorularının çözüm yöntemi aynıdır.
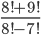 işleminin sonucu kaçtır?
işleminin sonucu kaçtır?
Kpss genel yenetek matematik dersinde faktöryelin bu tip sorularında büyük faktöriyel soruda bulunan en küçük faktöriyele indirgenip ortak çarpan parantezine alınır.
![]()
![]()
- (6-n)! ifadesinde n’in alabileceği kaç farklı değer vardır?
Faktöryel sayıları sadece doğal sayılardan oluşmaktadır. Dolayısıyla doğal sayılar kümesi dışında yer alan kavramlar faktöryel olamaz. Buradan n=0, 1, 2, 3, 4, 5, 6 değerlerini alabilir, yani n toplamda 7 değer alabilir.
- Matematik Sayılar Çözümlü soruları izlemek ve Sayılar İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Sayılar Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















